FrontPage kamelink
夏期 数学IIB頻出
【1】〜【2】指数・対数
【3】〜【5】三角関数
【6】〜【9】図形と方程式
【10】〜【12】ベクトル
【13】〜【16】数列
問題文をクリックすると解答をみることができます.
【1】(1) 指数方程式・対数方程式 †

指数方程式の基本問題です.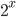 をひとかたまりに見て,2次方程式を解くことになります.
をひとかたまりに見て,2次方程式を解くことになります.

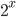 ,
,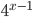 ,
,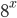 が登場します.まずは与式を
が登場します.まずは与式を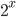 で整理しましょう.
で整理しましょう.

式変形の前に真数条件,底条件を抑えましょう.
【1】(2) 対数不等式 †

式変形する前に真数条件をおえましょう.

まずは底条件と真数条件を抑えます.その後は底を揃えると分数不等式の処理となります.

まずは真数条件,底条件をおさえましょう.つぎは底を揃えて進数を比較します.このとき底と1との大小関係に注意しましょう.
【2】 常用対数 †
- 十進法で表された自然数
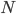 について
について

(1)真数5を 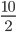 とみます.
とみます.
(2)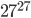 の桁数はこの数の常用対数の整数部分により決まります.
の桁数はこの数の常用対数の整数部分により決まります.

(1),(2)は頻出問題です.
(3)最高位から1つ下の位の数字を求めるのは珍しいですね.例えば,N=1234ならば求める数字は2です.これはNが1200≦N<1300であること,すなわち,1.2×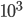 ≦ N<1.3×
≦ N<1.3×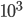 であることを確認することにより,求める数字が2であると分かります.
であることを確認することにより,求める数字が2であると分かります.
![[PukiWiki] [PukiWiki]](image/kame.png)
![[PukiWiki] [PukiWiki]](image/kame.png)