数学I・Aチェック＆リピート　第1章　§3集合と論理　1.集合，補集合

数学I・Aチェック＆リピート
式の値：無理数による対称式と交代式 ← 集合，補集合 → 必要・十分条件，同値

問題文をクリックすると解答をみることができます．

集合，補集合 †

類題演習 †

(２)ではド・モルガンの法則を用いましょう．(３)ではa<b<c<dが効いています．

24 共通テスト 本試験 I 1〔3〕
「X」と「Yの補集合」の共通部分はXからYの要素を除いた集合です．

倍数の個数はガウス記号を用いるとよいでしょう．

(２)はド・モルガンの法則を用いましょう．

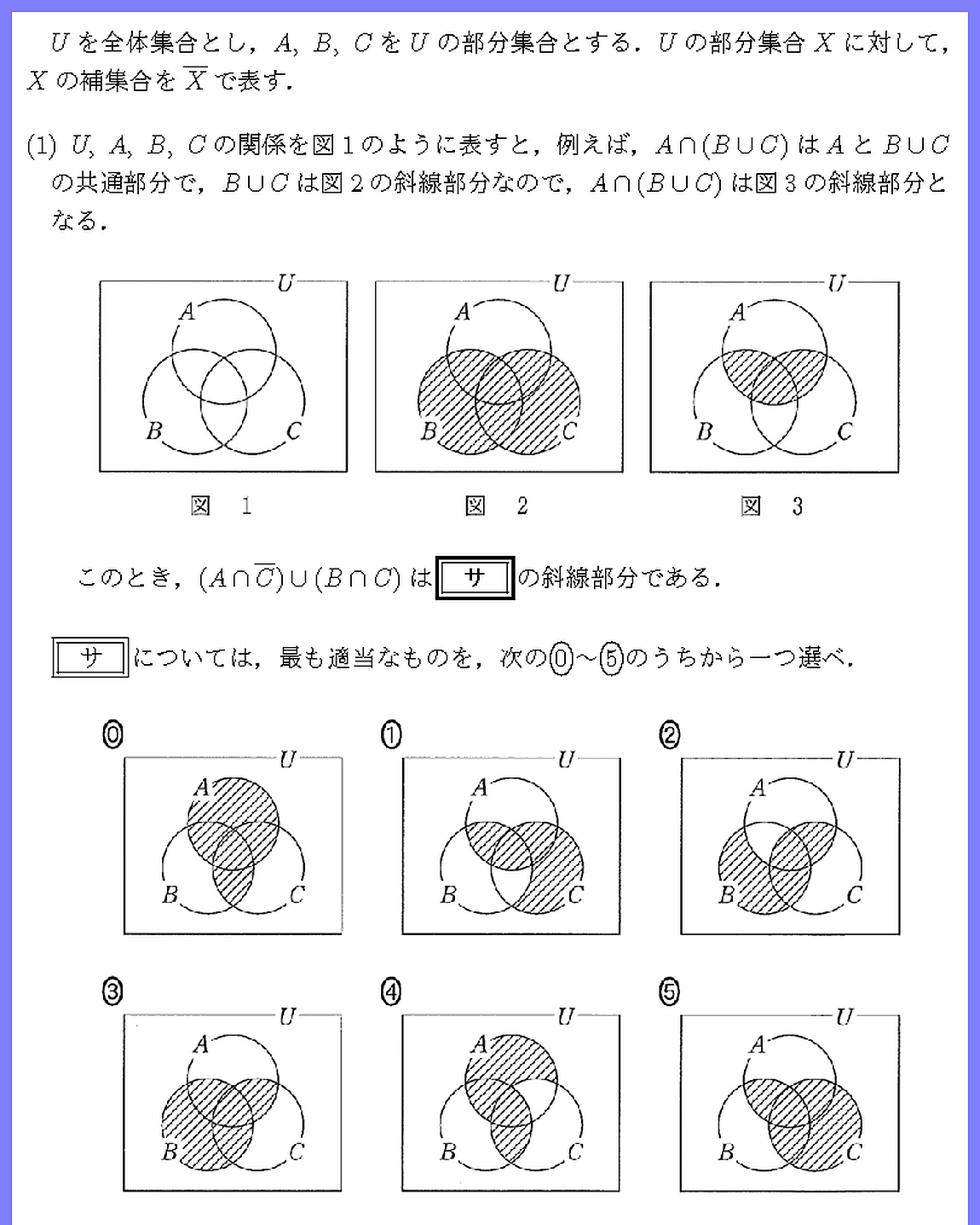
23 共通テスト 本試験 I 1[2]
集合，補集合を具体例で問うています．

集合A，Bを全体集合Uの中にベン図としてかいてみましょう．

Aは偶数，Bは3の倍数，Cは5の倍数の集合となっています．

集合も3つになると面倒ですね．(３)が面白い．

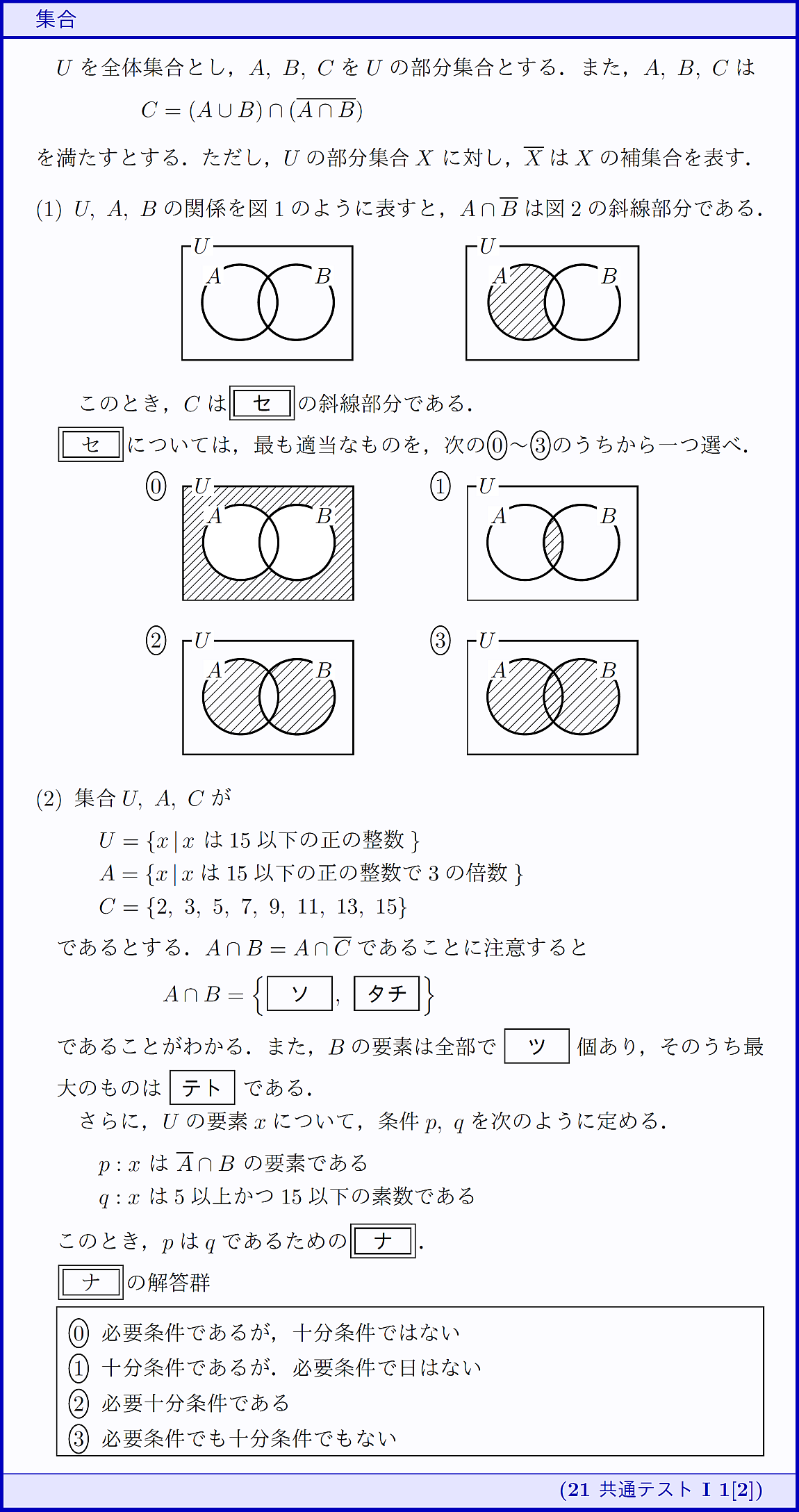
(１)は(２)のヒントになっています．
締めは定番の必要十分条件です．用語の使い方を間違えないようにしましょう．

3つの集合P，Q，Rの包含関係を捉えよう．
(3)は「p かつ q」である数について問われている．

(1)，(2)を解いた後に(3)だと，n(A)=0，１，…，5と場合分けしたくなりますが，
各要素がどの集合に属するかと視点を変えることも可能です．

X⊂Y ならば n(X)≦n(Y) が成り立ちます．
ベン図の利用も考えられます．

与えられた条件により a,b,c について3つの等式が得られます．

集合の演算の確認問題です．
ベン図を利用する手もあります．

3つの集合 A，B，Cの和集合は 2×2×2-1=７ 個の部分集合に分けることができます．
要素の個数について条件を連立方程式として表しましょう．

「かつ」，「または」の否定に関する演算の確認です．

英語が得意な人の集合と数学が得意な人の集合でベン図を描いてみましょう．

数学と英語の両方が得意な生徒の人数の範囲を求める．面白い設問になっていますね．

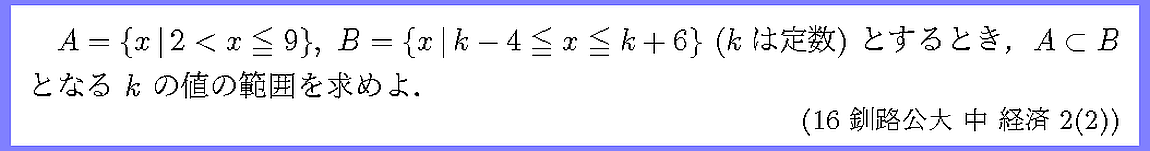
ｋについての不等式をつくる際には等号が付くか付かないかにも注意しましょう．

与えられた条件にド・モルガンの法則を用いてみましょう．