数学II・Bチェック＆リピート　第3章　§2方程式・不等式，最大・最小　2.方程式

数学II・Bチェック＆リピート
§2 方程式・不等式，最大・最小：周期とグラフ ← 方程式 → 不等式

問題文をクリックすると解答をみることができます．

方程式 †

類題演習 †

和を積に直す公式も使うか，2倍角・3倍角の公式を使うか．
積に直すことを考えるのだから和を積に直す公式も使う解法の方がストレートな解法でしょうか．

ｔとｘの対応関係に注意しましょう．

解と係数の関係を用いるとαについての連立方程式が得られます．

最後は三角関数を含む方程式を解きます．

三角関数を含む方程式の解の様子を問う良問です．

誘導にのり，f(ｘ)＝０ をｔで表し，ｔの値からｘを求めます．

三角関数を含む方程式の頻出問題です．(３)で cos α=cos 4α に気づけば(１)とつながります．

sin x，cos x の対称式は t=sin x+cos x とおきましょう．
tの値に対応するｘの個数に注意することが本問の要です．

ｔの値に対してθが何個対応するかをおさえましょう．

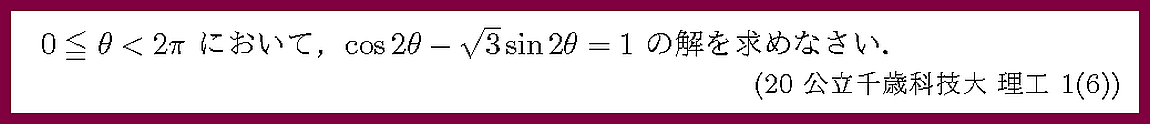
合成の公式を用いましょう．

いろいろな解法があります．

(2)は(1)を無視しても解くことができますが，(3)は(1)を利用しましょう．

角をそろえるように式を変形しましょう．
(2)は sin θの2次方程式として考えます．

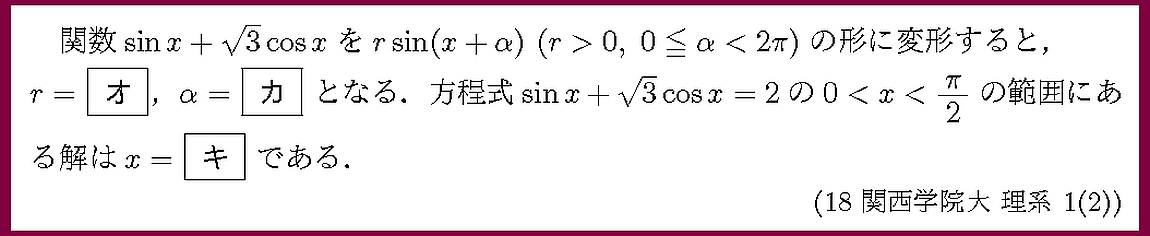
三角関数の合成を利用した方程式の問題です．

和積の公式を用いて式をまとめるとよいでしょう．
2倍角・3倍角の公式を用いてもよい．

αまたはβの消去を考えましょう．

和を積に直す公式を用いましょう．

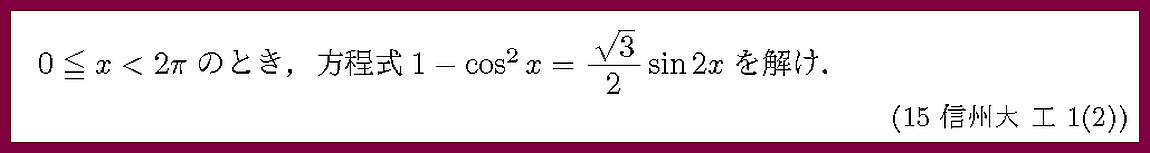
角をそろえることを考えましょう．

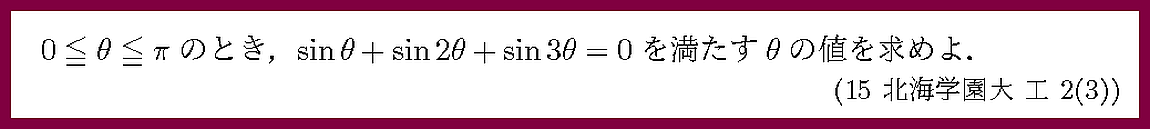
角をそろえることを考えましょう．

一般解を考えましょう．

(１)は(３)のヒントになっています．

角の範囲に注意しましょう．