数学II・Bチェック＆リピート　第8章　§2内積の計算　1.内積の計算

数学II・Bチェック＆リピート
領域の図示 ← §2 内積の計算：内積の計算 → ベクトルのなす角

問題文をクリックすると解答をみることができます．

内積の計算 †

類題演習 †

平方するか，直線のベクトル方程式とみるか．

(左辺)-(右辺)を計算しましょう．

内積の計算力が問われています．

２つの内積の値から△ABC の形状が決まります．

計算だけで処理できます．図形的には垂直二等分面，アポロ二ウスの球が登場します．

(１)はベクトルの成分表示を示唆しています．

(１)はベクトルの成分表示を示唆しています．

内積と分点公式が問われています．

内積についての計算力が問われています．

内積に関する計算を問うています．

(１)重心は公式として覚えておきましょう．
(２)面積TはSから余分な3つの三角形を除きましょう．
(３)どの頂角が直角となるかで場合分けしましょう．

内積の算出，垂直条件，長さの計算を問う内積の典型問題です．

(１)ベクトルの内積計算で出発していますが，
(２)(３)対称性のある三角関数の最大値，最小値を求める問題です．

|2a-b|を平方してみましょう．

(２)(３)では相加平均・相乗平均の関係を用いることができます．

内積の定義の確認問題です．

内積計算の確認問題です．

ベクトルの内積と大きさの計算が問われています．

四角形ABPCは円に内接する四角形であり，APは円の直径です．

内積の定義の確認問題です．余弦定理を用いましょう．

三角関数の合成となります．cos でまとめるか，sin でまとめるか．

与えられた条件には ∠AOC，∠BOC の情報があります．
これらから ∠AOB の cos ，sin を得ることができます．

(１)AP⊥AQを整理しておきましょう．(２)「P，Qの位置によらず」の扱いが問われています．

(２)では(１)をヒントとみるか，△ABEに着目するかで答えの形が変わります．

内積の計算問題です．与えられた条件はCを始点としたベクトルをとるように示唆している？

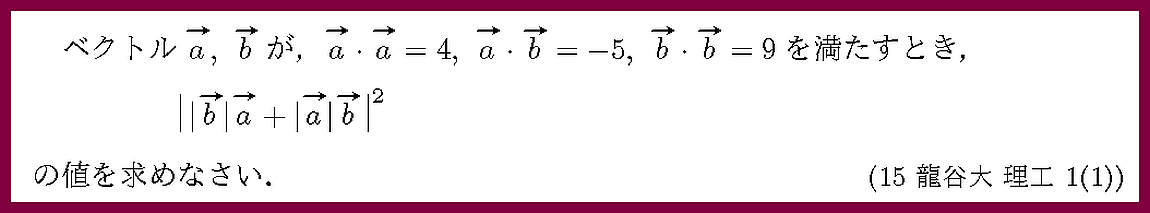
ベクトルの内積と大きさの関係の確認問題です．

内積の定義を問うています．ベクトルｐを(ｘ，ｙ，ｚ)と成分表示し，連立方程式をつくりましょう．