数学II・Bチェック＆リピート　第8章　§2内積の計算　4.三角形の面積

問題文をクリックすると解答をみることができます．

三角形の面積 †

三角形ABPの面積を最大にするPを図形的にとらえましょう．

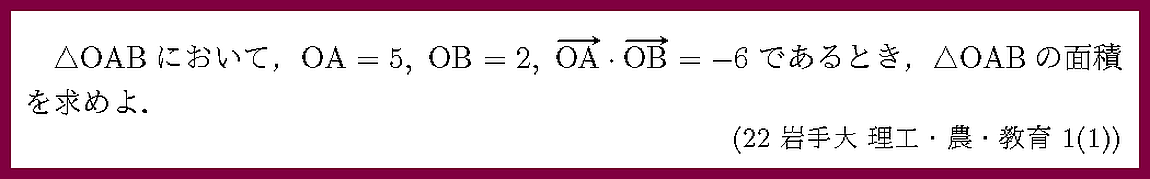
面積公式の確認問題です．

内積計算の確認問題です．

(４)1次独立性を用いるか，メネラウスの定理を用いるか．

(２)は(３)の誘導でしょうが，cosθをsinθに直さなければなりません．
ベクトルによる三角形の面積公式を用いましょう．

(１)は(２)の，(２)は(３)のヒントになっています．
(４)でのPの存在範囲をおさえるのがカギでしょうか．

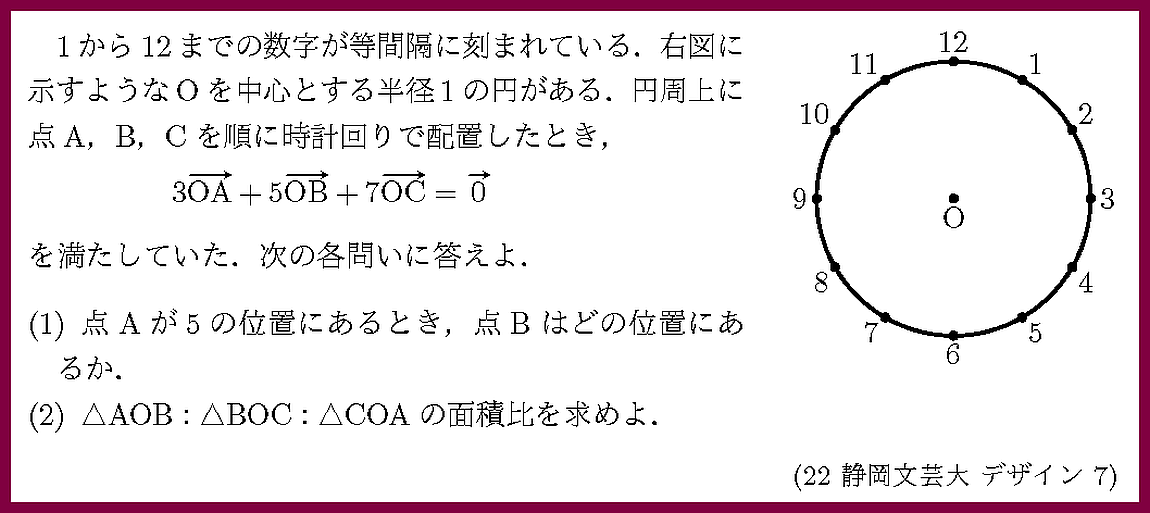
内積が分かれば角の情報が得られます．

(３)三角形の内接円の半径は三角形の面積を2通りに考えましょう．

共面条件と平行四辺形の面積が問われています．

与えられた条件よりベクトルOAはベクトルOB，OCで表すことができ，
点Pの位置を知ることができます．

点Pの動く範囲をおさえましょう．

正六角形は正三角形の寄せ集めであり，各点はベクトルOA，OEで表すことができます．

△OCDの面積は△OABの面積との関係を考えます．

(1)により△ABCの面積を求める準備が整いました．
(2)はｓ，ｔを係数とする2つの1次独立なベクトルの和と考えましょう．
これを基本ベクトルとした座標系を考えてPの動く部分を図示します．

内積と余弦定理は密接に関係しています．