数学IIIチェック＆リピート
r^n(n→∞),ハサミウチの原理
← 無限級数 →
無限等比級数
問題文をクリックすると解答をみることができます．
無限級数 †
類題演習 †
無限級数の和の定義を確認しておきましょう．
(３)無限和の面白さを堪能しましょう．
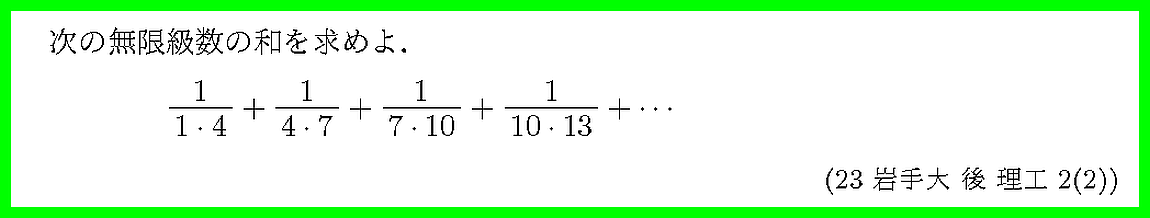
まずは一般項を確定し，つぎに第ｎ部分和を求めましょう．
誘導にのり進んでいきましょう．
(２)では(１)の不等式を利用してはさみうちの原理を用います．
推定が1つのヤマです．この手の推定は珍しい．
(1)は数学的帰納法を用います．(2)では「＜２」であり「≦２」でないことに注意しましょう．
Σ(１/k^2）はゴミはゴミ，Σ(１/k）はチリも積もれはヤマとなるの代表例です．
無限級数では部分和の極限を考えます．
(１)は ｙ＝１/ｘ のグラフと関連付けましょう．
無限級数として処理するか，複素数をもち出してド・モアブルの定理を利用するか．
分母を階差に分解して，式を整理します．
部分和の極限を考えましょう．
(６)はバーゼル問題と呼ばれています．
無限和が存在する条件は部分和の極限が存在することです．まずは部分和を整理しましょう．
ａ＿ｎ は -1/2，-1/2，1 を繰り返します．
ｎを3で割った余りで場合分けして部分和を計算しましょう．
![[PukiWiki]](image/kame.png "[PukiWiki]")
