数学IIIチェック＆リピート　第5章　§1積分の計算　11．定積分と漸化式

数学IIIチェック＆リピート
定積分で表された関数 ← 定積分と漸化式 → 区分求積

問題文をクリックすると解答をみることができます．

定積分と漸化式 †

類題演習 †

式を整理するとｎの分数式となります．(ｎの実数乗)の極限を確認しておきましょう．

部分積分，置換積分の計算力が問われています．

医(生命・保健)・工と医(医)で若干I＿ｎが違っています．

医(生命・保健)・工と医(医)で若干I＿ｎが違っています．

この手の積分の一般化も考えてみましょう．

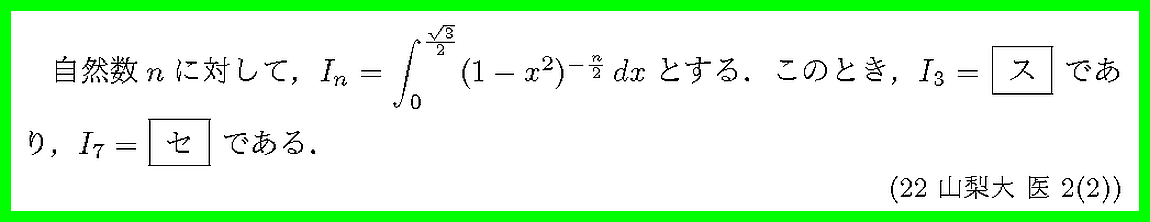
与えられた定積分について漸化式をつくりましょう．

(５)でI＿ｎが確定します．

b＿{n+1}=b＿{n}+(定数)として階差が与えられています．

(２)部分積分法を用いて漸化式をつくりましょう．

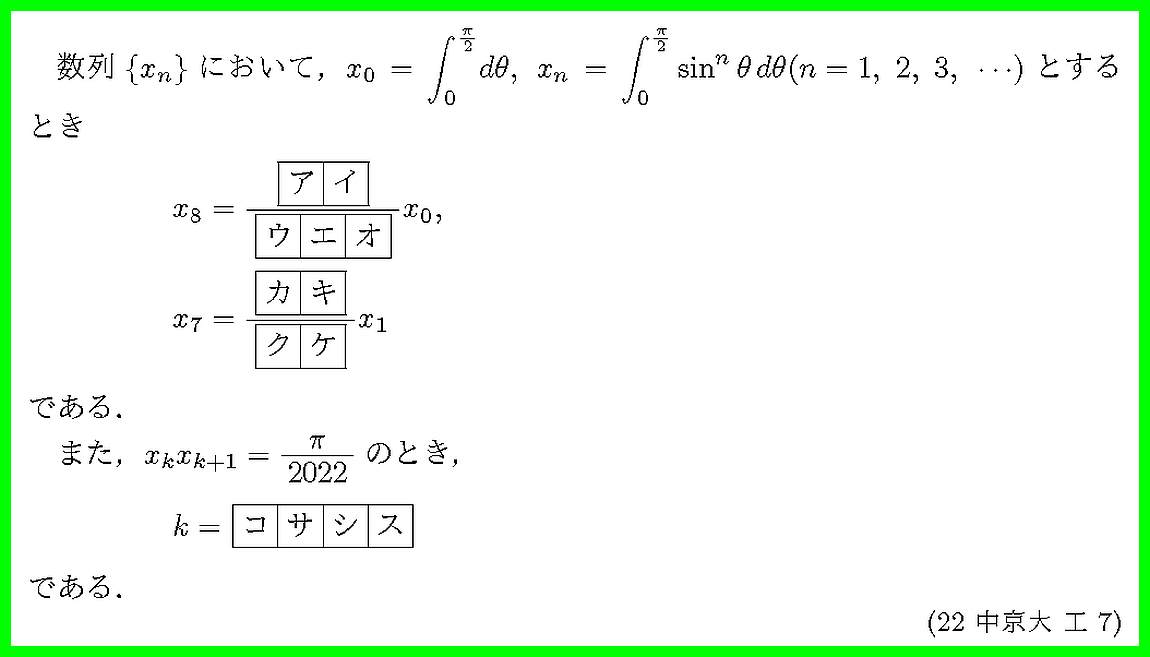
部分積分法を用いて漸化式をつくりましょう．

(３)での積分は2つ飛びの漸化式になっています．

定積分と漸化式についての典型問題です．部分積分法を用います．

(３)でははさみうちの原理を用います．

(３)へのつながりが面白いですね．

(１)，(２)は置換積分，(３)は部分積分を用います．
さて，(４)はどうしますか？

計算力が試されています．
問題の流れにのることができるのも実力の証しです．

(1)は置換積分法(2)は部分積分法を用いましょう．
(3)の前半は(2)を利用しますが，後半は「はさみうち」を用います．

β(べータ)関数の扱いに慣れましょう．

部分積分を実行して漸化式をつくります．