数学I・Aチェック＆リピート
1次関数の最大・最小
← 2次関数の最大・最小 →
2次関数の最大・最小(場合分け，置き換え)
問題文をクリックすると解答をみることができます．
2次関数の最大・最小 †
類題演習 †
すべてのｘに対して f(x)≧m が成り立ち，f(x)=m を満たすとき，ｍ を f(ｘ) の最小値といいます．
整数を定義域とする２次関数の最大・最小が問われています．軸の位置に着目しましょう．
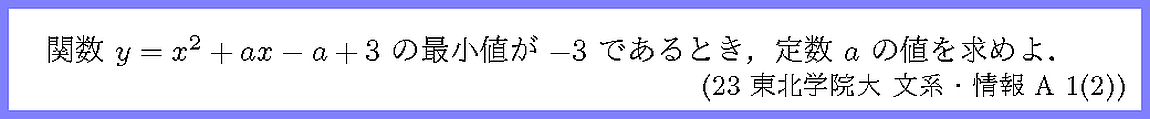
平方完成してｙの最小値をａで表しましょう．
(１)，(２)ともにグラフを描きましょう．
すべてのｘに対して f(x)≧m が成り立ち，f(x)=m を満たすとき，ｍ を f(ｘ) の最小値といいます．
−２≦ｘ≦２におけるｙ＝ｈ（ｘ）のグラフを描きましょう．
定義域に注意して，グラフを描きましょう．
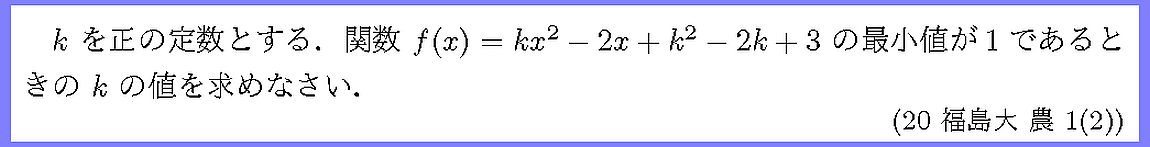
実数全体で定義された2次関数のグラフが下に凸であるとき，
２次関数の最小値は頂点のｙ座標です．
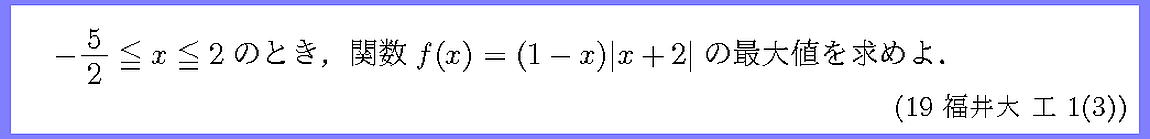
場合分けして絶対値を外し，グラフを描きましょう．
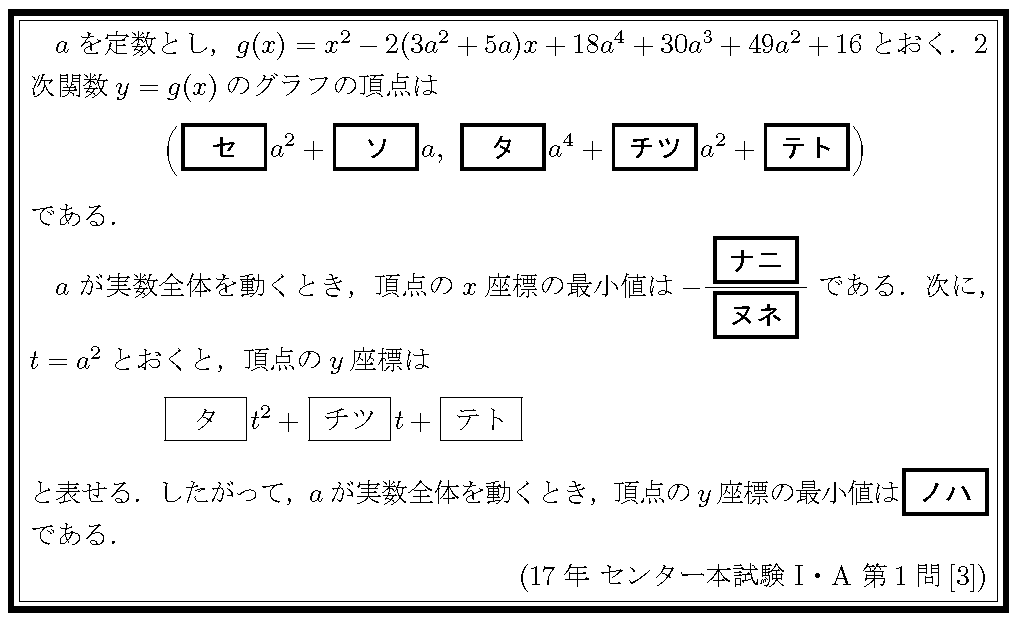
最小値は軸の位置に着目しましょう．頂点の座標は２次式の平方完成を利用します．
![[PukiWiki]](image/kame.png "[PukiWiki]")
