数学I・Aチェック&リピート
積の法則,一筆書き
← 塗り分け →
かく乱順列
問題文をクリックすると解答をみることができます.
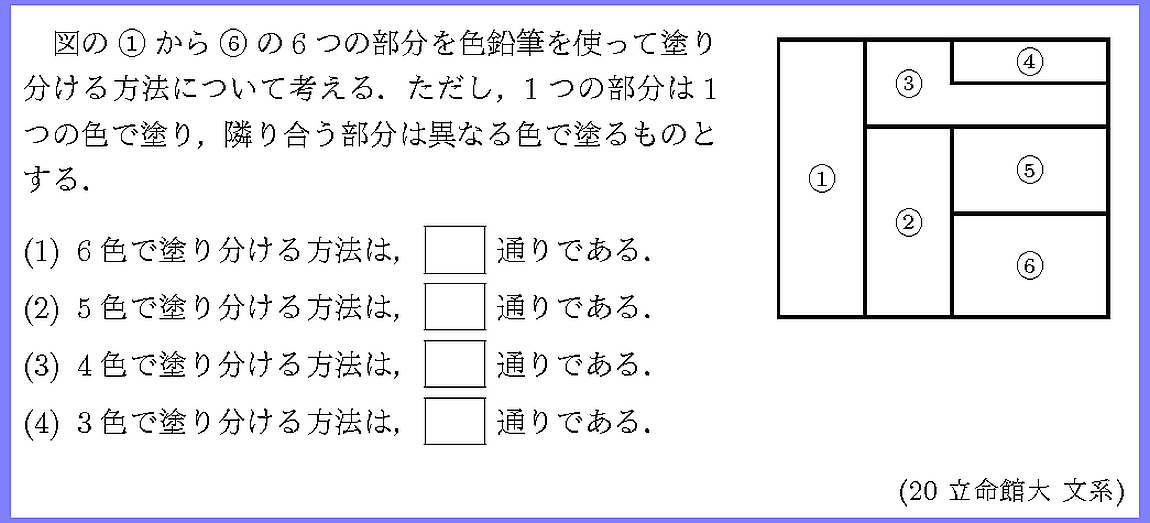
塗り分け †
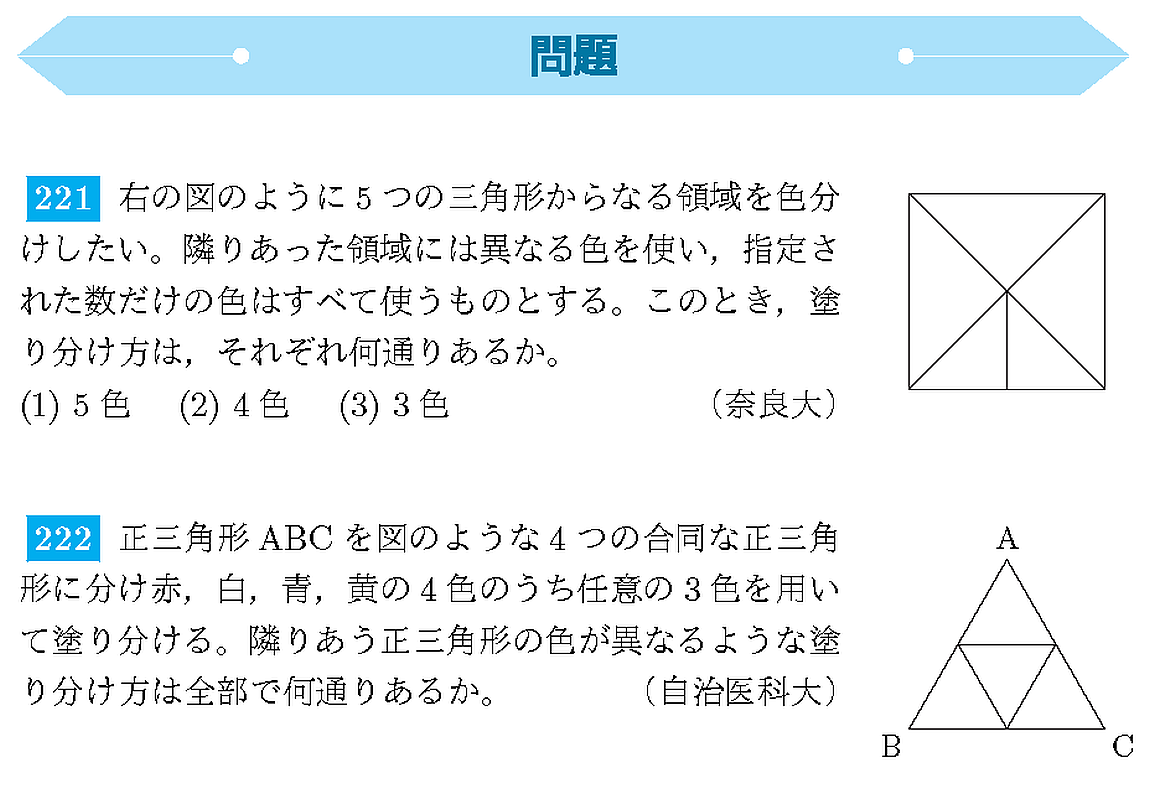
類題演習 †
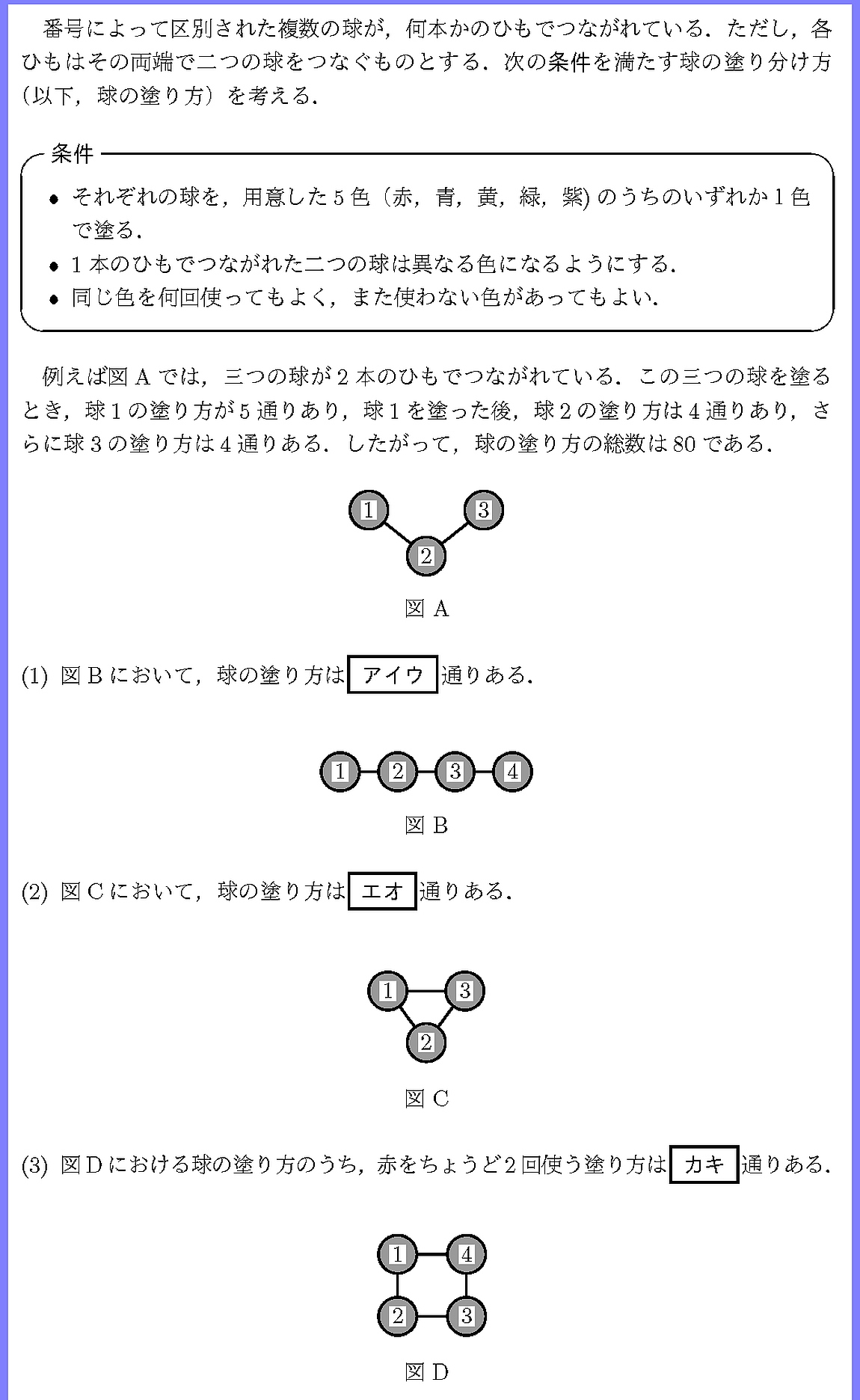
23年 共通テスト本試験 IA 第3問
親切な誘導にのって進みましょう.(6)は(5)の考え方を真似ましょう.
(1)は6色の順列でよいのですが,
(2)以降は同じ色を塗る部分が2か所あるいは3か所出てきます.

小三角形に名前を付けて隣り合う小三角形は異なる色となるように塗り分けていきましょう.
3色すべてを使うことも忘れないようにします.

安易に「円順列だから」,「数珠順列だから」と処理するわけにはいきません.
どのような回転で一致するのか丁寧に調べていきましょう.

(2)番号1の向かい側の頂点の番号を決めると残り4個の番号は円順列です.
(3)2つの面の位置関係は,共有点なし,1点を共有,1辺を共有の3通りです.
(4)3つの面について共有辺となる辺の個数は0,1,2のいずれかです.
![[PukiWiki] [PukiWiki]](image/kame.png)
![[PukiWiki] [PukiWiki]](image/kame.png)