数学I・Aチェック＆リピート　第8章　§2独立試行・反復試行　4.いろいろな独立試行・反復試行

問題文をクリックすると解答をみることができます．

いろいろな独立試行・反復試行 †

24 共通テスト本試験 IA 3
親切な誘導が付いた問題です．

(２)をどう処理するか？

確率というより絶対値の処理に重点が置かれた問題です．

最大確率はａを実数とみて微分を利用しましょう．

(１)は(３)の誘導になっています．

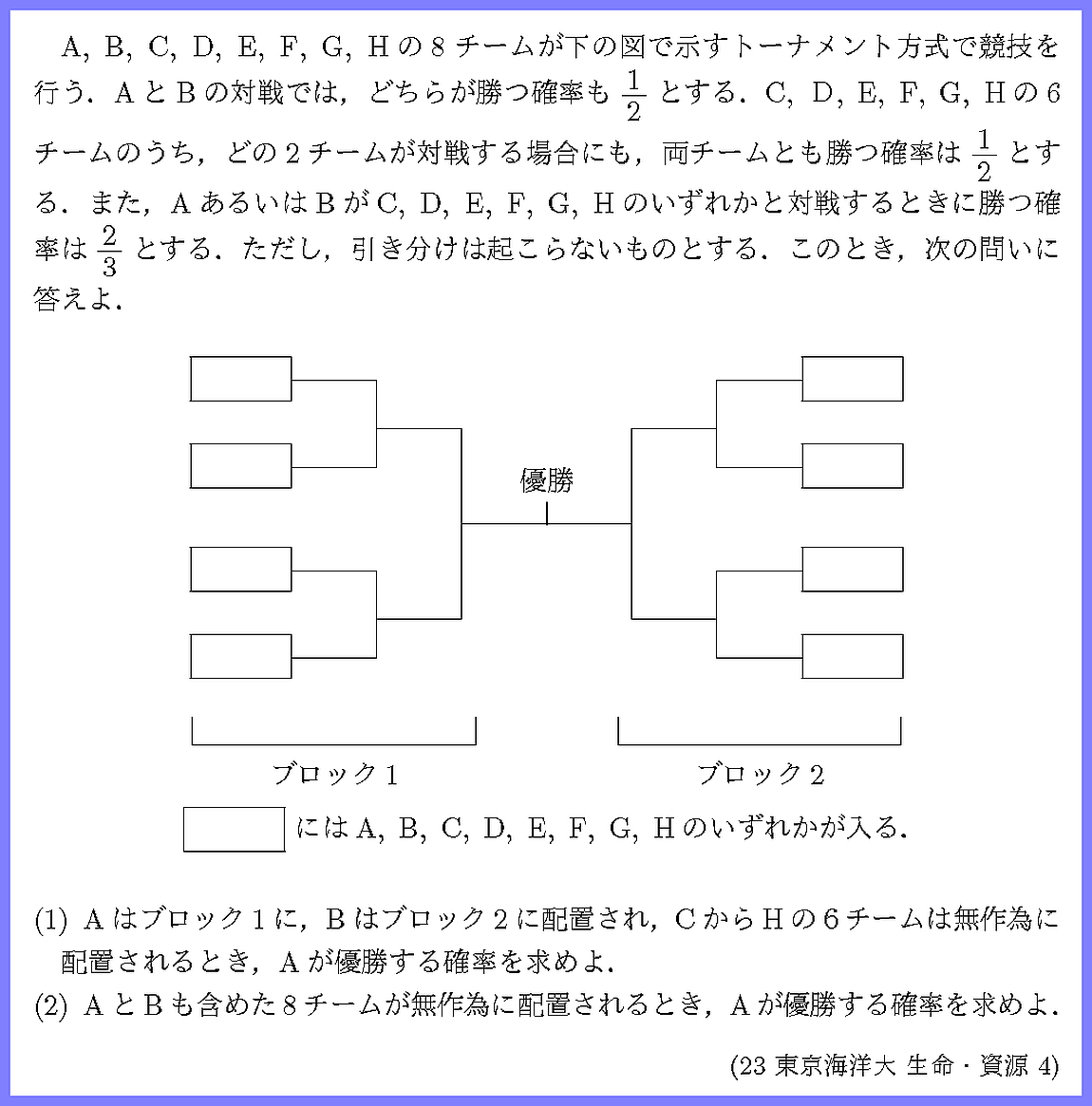
(１)は(２)の準備です．AとBの対戦状況を把握しましょう．

(２)(ii)は最大確率を求めるときの常套手段です．

条件を満たす状況を把握し場合の数を求めましょう．

N巡目以内に勝者になる確率では等比数列の和の公式を用います．

ｎ－１回目までに白玉，青玉，黄玉がすべて取り出されていて，
ｎ回目に初めて赤玉が取り出されるということです．

(２)は(３)の準備です．比を利用して確率の増減を調べます．

(2)は余事象を考えましょう．
(3)は余事象を考えるか，5が何回出るかで場合分けするかでしょう．

条件を満たす組(ａ，ｂ，ｃ)が決まれば各数字が書かれたカードをとる確率はつねに１／７です．

A，Bそれぞれの得点を調べ上げましょう．
サイコロ投げとコイン投げは独リな試行であり，A，Bの得点のとり方も独立な試行です．

(i)は「同様の確からしさ」の確認です．
(ii)は1回の試行で３種類の事象が起こる反復試行の確率です．

ｎ回目の票読みでのP，Qが得た票数を組としてｘｙ平面上にとると最短経路の問題に帰着されます．