数学IIIチェック＆リピート
極形式
← ド・モアブルの定理 →
1のn乗根の図示
問題文をクリックすると解答をみることができます．
ド・モアブルの定理 †
類題演習 †
(１)はド・モアブルの定理，(２)(３)は極形式について問うています．
与式は等比数列の和です．
(１)をヒントにSを2通りに計算してみましょう．
円，垂直二等分線の共有点について問われています．
(2)極形式で表すとド・モアブルの定理を用いることができます．
ド・モアブルの定理を利用しましょう．(３)は三角形の特徴をつかみましょう．
ド・モアブルの定理を用いましょう．
ド・モアブルの定理を用いましょう．
ｚを極形式で表し，ド・モアブルの定理を用いましょう．
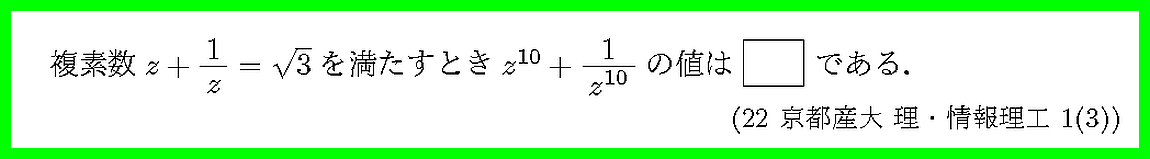
解法は(zのｎ乗)+1/(zのｎ乗)を順次つくっていくか，ド・モアブルの定理を利用するか,
で分かれるでしょう．後者の解法の方が拡張性があります．
極形式に直してド・モアブルの定理を用いましょう．
虚数のｎ乗は極形式に直してド・モアブルの定理を用いましょう．
極形式，ド・モアブルの定理，解と係数の関係など複素数計算の項目がテンコ盛りです．
ド・モアブルの公式，べき乗の指数計算，三角関数の公式，極限などの
総合的な計算力が問われています．
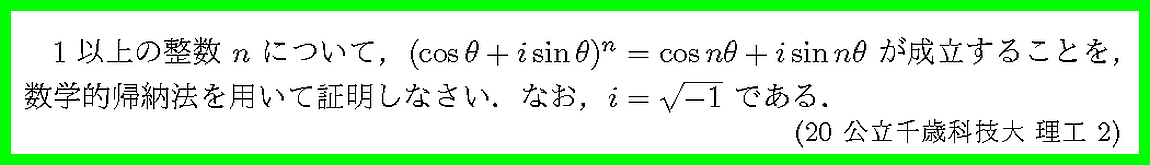
ド・モアブルの定理の証明です．
ド・モアブルの定理を用いましょう．
![[PukiWiki]](image/kame.png "[PukiWiki]")
