数学IIIチェック＆リピート
§1 積分の計算：積分の計算
← 置換積分 →
部分積分
問題文をクリックすると解答をみることができます．
置換積分 †
類題演習 †
置換積分法を用いましょう．
置換積分法を用いましょう．
ｇ(ｘ)は偶関数で，ｈ(ｘ)は奇関数です．
(３)ではｆ(ｘ)を偶関数，奇関数に分解して積分することを求めています．
ａからｂまでのΔｘによる積分をｂからａまでの（-Δｘ）による積分としたのが本問です．
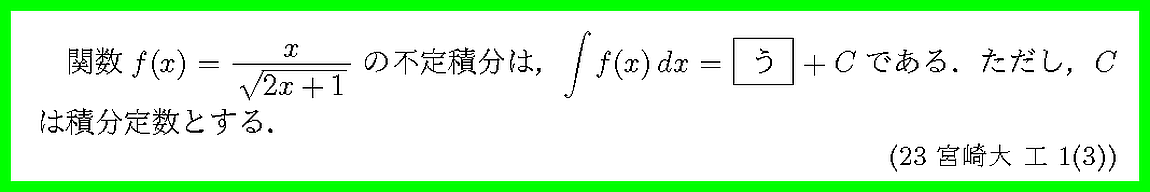
置換積分法を用います．
置換積分法を用います．
置換積分法を利用します．
円の扱い方と積分の計算力が問われています．
置換積分法を用いましょう．
置換積分法を用いましょう．
(１)は置換積分です．(２)は(１)を利用します．
(２)では(１)の利用を考えます．
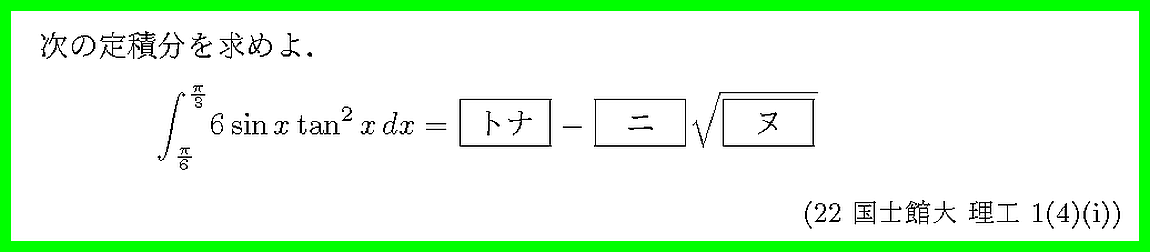
tan xの微分を思い出して，置換積分しましょう．
もちろん，置換積分法を用います．
置換積分法を用いましょう．
置換積分法を用います．
絶対値をはずすために積分区間を分けましょう．
置換積分法を用います．
置換積分法を用いましょう．
(１)は(２)のヒントです．
置換積分法を用います．では，どのような置換を考えるか？
(2次式)/(2次式)なので割り算を実行します．ｔ＝２ｘ＋１と置き換えから割り算するとよいでしょう．
置換積分法を用いましょう．
置換積分の基本問題です．
置換積分法を用いましょう．
(2)は(3)のヒントです．(3)では(2)が使えるように変形しましょう．
さて，どうやるか？F(２)はF(ｋ)を求めるヒントでしょう．
置換積分を用います．
置換積分法を用います．
(１)割り算を実行しましょう．(２)置換積分法を用います．
置換積分法を用います．
置換積分法を用います．
置換積分法を用いましょう．
1-1problem.png "問題文をクリックしてみて下さい．")
(ｂ)(ｃ)は(ａ)をヒントにして，セットで考えましょう．
(ｂ)は被積分関数をｙとｙ’で表してみましょう．
分子は分母の微分となっています．(瓶詰め型の)置換積分法を用いましょう．
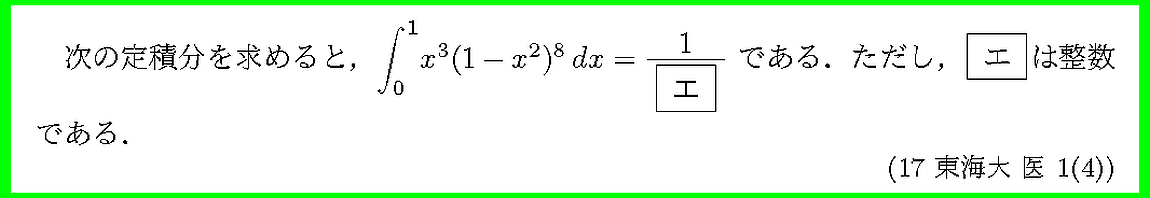
置換積分の基本問題です．
公式の確認問題です．
![[PukiWiki]](image/kame.png "[PukiWiki]")
