北海道大学

FrontPage

このページでは「北海道大学」の過去問を扱っています．

令和５年度一般選抜個別学力検査等（前期日程・後期日程）の試験問題および正解・解答例等は、 令和5年5月31日〜9月30日まで掲載されています．
入試データ：過去5年分の 「入学志願者数及び合格者数等一覧」と「合格者の平均点等一覧」をみることができます．

ブックマーク †

/大学入試数学問題集成：札幌農学校時代からの問題が収録されています(1901〜)．

問題番号「【？】」の部分をクリックすると問題文と解答例を見ることができます．

2024年 †

• 理系前期
  【１】　数II(三角関数，図形と方程式)　三角関数の連立方程式，点の軌跡
  【２】　数A(確率)　正八面体のさいころによる条件付き確率
  【３】　数II(積分)　定積分で表された関数列(定数型)
  【４】　数B(平面ベクトル)　三角形の内心
  【５】　数III(積分)　曲線の接線と面積
  
• 理系後期
  【１】　数III(積分)　積分を含む数列の極限
  【２】　数II(方程式)　整数となる分数式
  【３】　数III(複素数)　複素数での連立方程式
  【４】　数III(積分)　x軸，y軸まわりの回転体の体積
  
• 文系前期
  【１】　数A(整数)　約数の個数と総和
  【２】　数B(数列)　２項間漸化式
  【３】　数II(積分)　３次関数のグラフと面積
  【４】　数A(確率)　正八面体のさいころによる確率
  

2023年　 †

• 理系前期 出題意図・採点講評
  【１】　数III(複素数平面)　円の方程式，極限
  【２】　数B(空間ベクトル)　球面と平面，球面と直線の位置関係
  【３】　数III(微分)　ｘ，ｙについての指数方程式
  【４】　数A(確率)　さいころの目と絶対値の和についての確率
  【５】　数III(微分)　直線に関する対称点と共線条件，関数の増減
  
• 理系後期 出題意図・採点講評
  

• 文系前期 出題意図・採点講評
  【１】　数II(整式)　恒等式
  【２】　数B(平面ベクトル)　内角，外角の2等分線
  【３】　数A(確率)　さいころの目と絶対値の和についての確率
  【４】　数II(積分)　放物線と円で囲まれた領域の面積
  

2022年　 †

• 理系前期　 出題意図・採点講評
  【１】　数I(2次関数)　2変数関数|x(x-1)|+|(x-a)(x-b)|の最大・最小
  【２】　数B(数列)　ベクトル表記された３項間漸化式
  【３】　数III(微分積分)　面積の最小
  【４】　数A(確率)　円順列を舞台にした条件付き確率
  【５】　数III(複素数平面)　円と垂直二等分線の共有点
  
• 理系後期　 出題意図・採点講評
  【１】　数A(整数)　3元3次の不定方程式
  【２】　数II(図形と方程式)　不等式で表された領域と論証
  【３】　数II(図形と方程式)　垂直二等分線が3本存在する条件
  【４】　数III(複素数平面)　極形式，直線の動く範囲
  
• 文系前期　 出題意図・採点講評
  【１】　数II(不等式)　因数定理と3次不等式
  【２】　数B(漸化式)　階差が与えられた数列の一般項と最小値について
  【３】　数I,II(三角比)　内接円の半径，sin15°
  【４】　数A(確率)　A，B，Cが書かれたカード10枚による条件付き確率
  

2021年　共通テスト開始 †

• 前期　出題意図・講評
• 理系前期
  【１】＞ 文【１】　数B(平面ベクトル)　正射影ベクトル
  【２】　数II(微分)　放物線と接線，長さの比の最小値
  【３】　数II(対数)　対数の最大値，相加平均・相乗平均
  【４】　数B(数列)　連立漸化式と数学的帰納法
  【５】　数III(積分)　パラメータ表示された曲線と面積
  
• 理系後期
  【１】　数II(積分)　４次関数のグラフと接線で囲まれた部分の面積
  【２】　数B(平面ベクトル)　共線条件とベクトルの大きさ
  【３】　数A(確率)　4種類のカードによる条件付き確率
  【４】　数A(整数)　4を法とする合同式
  
• 文系前期
  【１】　数B(数列)　和と一般項の関係
  【２】＜ 理【１】　数B(平面ベクトル)　正射影ベクトル
  【３】　数II(三角関数)　三角関数を含む方程式，２倍角の公式
  【４】　数II(積分)　放物線と直線で囲まれた部分の面積
  

2020年　後期日程の個別学力検査等は中止 †

• 理系前期
  【１】　数B(平面ベクトル)　円に内接する四角形
  【２】　数A(整数)　直線上の格子点
  【３】＞文[3]　数A(確率)　さいころ投げによる最大公約数・最小公倍数
  【４】　数III(数列の極限)　漸化式とハサミウチの原理
  【５】　数III(積分)　面積と極限
  
• 文系前期
  【１】　数II(図形と方程式)　放物線と直線
  【２】　数II(三角関数)　三角関数で表された方程式の解の個数(置き換え)
  【３】＜理[3]　数A(確率)　さいころ投げによる最大公約数
  【４】　数II(積分)　２つの放物線に接する直線と面積
  

2019年 †

• 理系前期
  【１】≒文【１】　数B(空間ベクトル)　垂線の足が三角形の周，内部にある
  【２】　数A(整数)　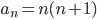 と 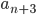の最大公約数について
  【３】　数III(微分)　関数 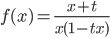の極値を与える点を結ぶ線分の中点
  【４】　数A(確率)　2つの箱から番号札を取り出すときの得点の確率
  【５】　数III(積分)　定積分で表された関数の列
  
• 理系後期
  【１】　数A，III(確率，極限)　持ち点の極限
  【２】　数II(図形と方程式)　三角形の重心の軌跡
  【３】　数III(複素数平面)　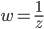による円の像
  【４】　数III(積分)　面積
  

• 文系前期
  【１】≒理【１】　数B(空間ベクトル)　垂線の足が三角形の周，内部にある
  【２】　数II(三角関数)　2直線のなす角
  【３】　数B(漸化式)　和がｎとなる1，2の列の個数，3項間漸化式
  【４】　数II(微分)　異なる3つの実数解をもつ3次方程式
  

2018年 †

• 理系前期
  【１】　数B(空間ベクトル)　2直線の最短距離
  【２】　数III(複素数平面)　ジューコフスキー変換
  【３】　数A(確率)　4枚のカードでつくられる数が9の倍数である確率
  【４】　数II(図形と式)　不等式で表された領域
  【５】　数III(微分，積分)　微分法の不等式への応用，面積
  

• 理系後期
  【１】　数A(整数)　ガウス記号
  【２】　数III(複素数平面)　三角形の重心の軌跡
  【３】　数B(漸化式)　確率と漸化式，ポリアの壺
  【４】　数III(積分)　カテナリーの弧長，軌跡
  

• 文系前期
  【１】　数I(三角比)　余弦定理
  【２】　数I(2次関数)　2次関数の最小値
  【３】　数A(確率)　3色のサイコロによりつくられる数についての確率
  【４】　数II(積分)　3次関数と2次関数のグラフが囲む部分の面積
  

2017年 †

• 理系前期
  【１】≒文1　数A(整数)　平方数
  【２】　数III(積分)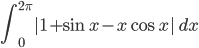　
  【３】　数III(複素数平面)　三角形の外心
  【４】　数A(確率)　数直線上の移動
  【５】　数II(図形と式)　不等式の表す領域
  
• 理系後期
  【１】　数A(図形の計量)　直三角柱の内部に含まれる球の半径
  【２】　数III(積分)　cosθの２ｎ乗の定積分
  【３】　数III(数列の極限)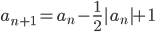　
  【４】　数II(図形と式)　放物線と直線，領域における最大・最小
  
• 文系前期
  【１】≒理1　数A(整数)　平方数
  【２】　数B(平面ベクトル)　円と内積
  【３】　数B(確率と漸化式)　正四面体の頂点を移動する点
  【４】　数II(積分)　定積分で表された関数，極大値の存在条件