数学II・Bチェック&リピート
2数を解とする2次方程式
← 高次方程式 →
3次方程式の解と係数の関係
問題文をクリックすると解答をみることができます.
高次方程式 †

類題演習 †

与えられた等式は9個の値k=0,1,…,8に対して成り立っています.

(*)は相反方程式とよばれています.
(4)では4つの解がすべて異なることを示すことを忘れないようにしましょう.

因数分解を実行しましょう.

まずは2次式の積に因数分解しましょう.
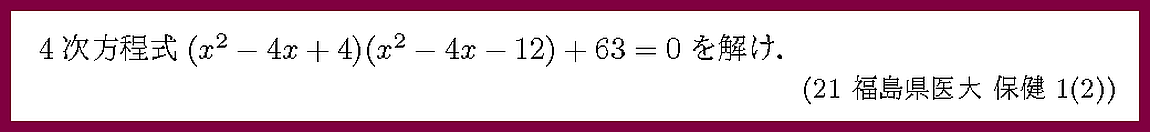
式の変形を工夫しましょう.

相反方程式の実数解を問うています.

3次方程式の興味ある解法ですね.

与えられた変形は相反方程式での常套手段です.
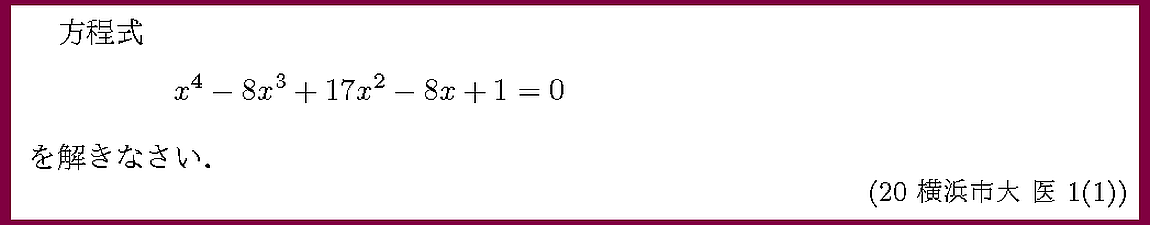
これは相反方程式と呼ばれる方程式です.

4次式を平方の差に分解して因数分解するというフェラーリの解法が誘導されています.
1-2problem.png)
展開の組合せを工夫しましょう.

整式P(x)について,方程式P(x)=0がx=αを重解にもつということは,
P(x)が(x−α)^2で割り切れるということです.

αの出所は3次方程式の公式(カルダノの公式)ですね.
2015年横浜市大・医3で同じ値が登場します.
2009年東北大後期理系3も参照してください.

(1)の結果は(2),(3)で効いてきます.
![[PukiWiki] [PukiWiki]](image/kame.png)
![[PukiWiki] [PukiWiki]](image/kame.png)