数学I・Aチェック＆リピート
和事象の確率
← さいころの確率 →
赤玉，白玉の確率
問題文をクリックすると解答をみることができます．
さいころの確率 †
類題演習 †
条件を満たす組(a,b)を拾いあげます．
出る目の和が６となる数字の組合せを拾いあげましょう．
正確な数え上げが問われています．
確率の問題ですが，2次方程式の実数解，解の配置のウェートの方が大きいです．
１，２，７，８の目に着目しながら2種類のさいころの目の出方を数えていきます．
ｎ個のサイコロの最大目をXとしたとき，
Xがkである確率 P(X=k) は P(x=k)=P(x≦k)-P(x≦k-1) です．
出た目の最大値が5，最小値が2であるということは，
3個のサイコロの「すべての目は2以上5以下であり」
かつ「少なくとも1つ5の目が出て」
かつ「少なくとも1つ5の目が出る」ということです．
条件をみたすサイコロの目の出方をとらえましょう．
判別式＝０，＞０となる組（ａ，ｂ，ｃ）をコツコツ数えます．
(1)は(2)のヒントです．
(2)では3個の目の出方が６通りとなるような目の積の値ｋを求めることになります．
3個の目の出方は同じ目がない，2個ある，3個とも同じ目であるの３通りに場合分け出来ます．
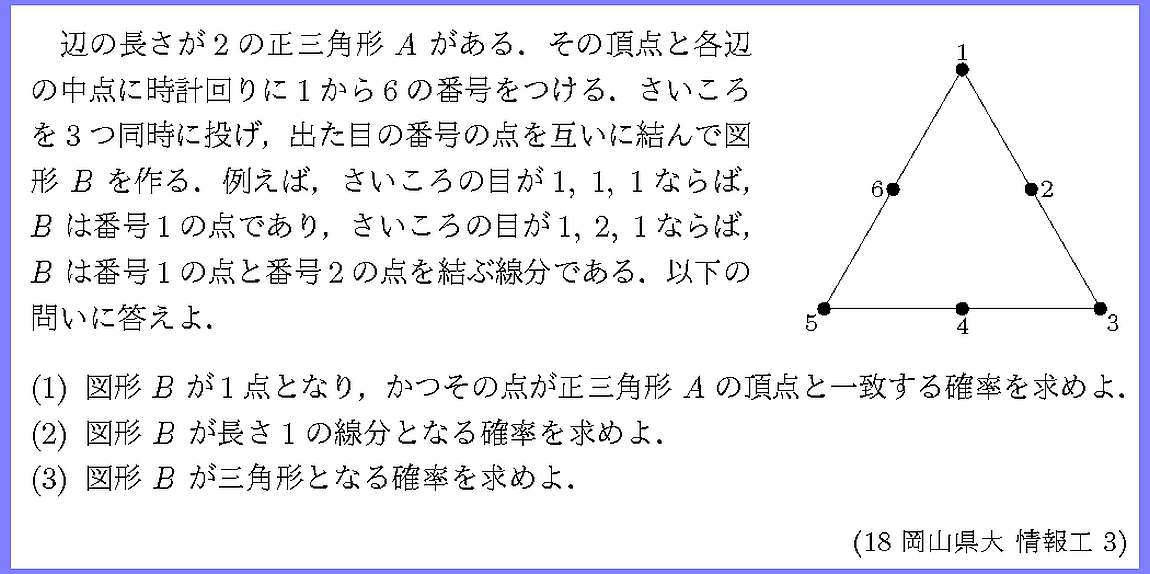
(3)は余事象でいくか，直接数えるか．
(3)得点の決め方が2種類あることに注意します．
Mが奇数となるのはすべて目が奇数のときです．
Mを3で割ったときの余りについては1〜6を3で割った余り0，1，2の積を考えましょう．
![[PukiWiki]](image/kame.png "[PukiWiki]")
