数学II・Bチェック＆リピート
直線
← 平面 →
球面
問題文をクリックすると解答をみることができます．
平面 †
類題演習 †
(１)ひし形をどうとらえるか．(２)はいろいろな解法が考えられそうです．
点Pが平面 ABC 上にあることを式で表しましょう．
ベクトルADをベクトルABとベクトルACで表しましょう．
OPは直角三角形OHPの斜辺になっています．
三角形の内部または周にあるという条件をどう処理するか．
前半は法線ベクトルを利用して点と平面との距離を求めようとしています．
直線と直線の交点，垂直条件，直線と平面の交点など空間座標でのいろいろなテーマを問うています．
いろいろな解法が考えられます．平面を扱うときの道具を確認しておきましょう．
点Dが平面ABC上を動く条件は？
平面に下した垂線の長さを求めていますが，(１)の誘導はない方が解法が広がります？
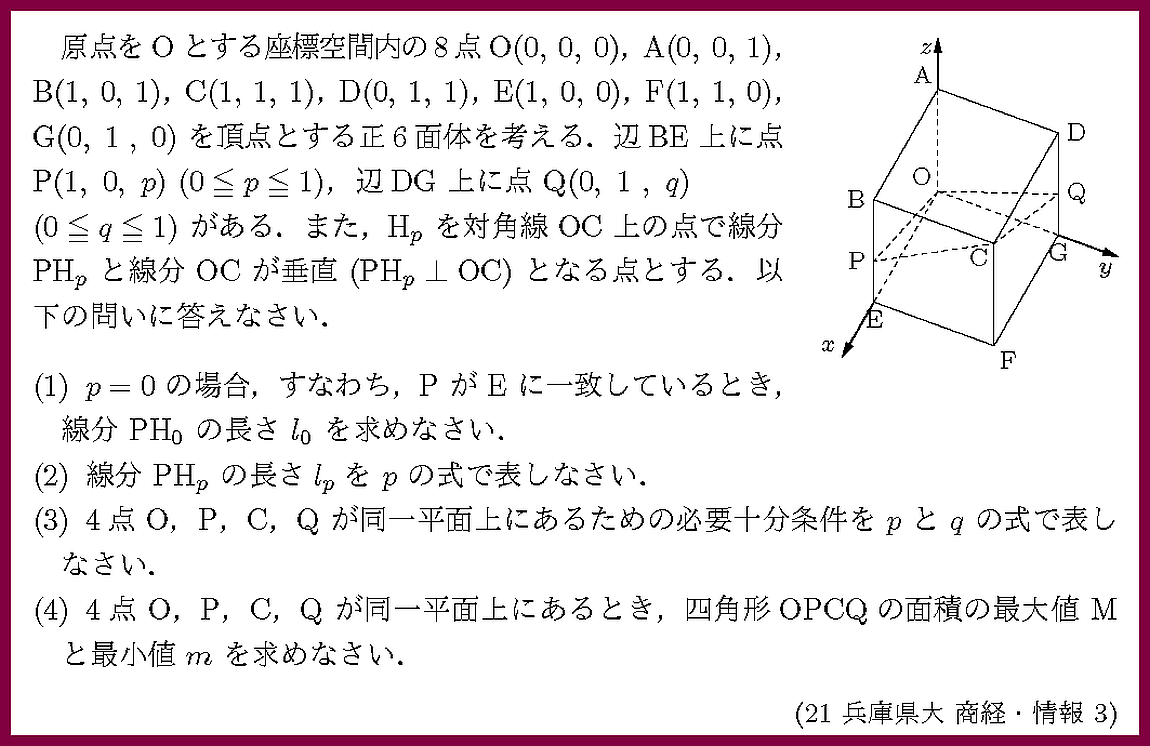
共面条件，面積が問われています．
Pは平面ABC上の点として与えられています．
(１)点Pが平面 ABC 上にあるとき，ベクトルAPは
ベクトルAB とベクトルAC の一次結合で表すことができます．
(２)垂直条件は 内積=0 を利用しましょう．
また，(１)，(２)は法線ベクトル，正射影ベクトルを用いた別解もあります．
平面を表すベクトル方程式を確認しておきましょう．
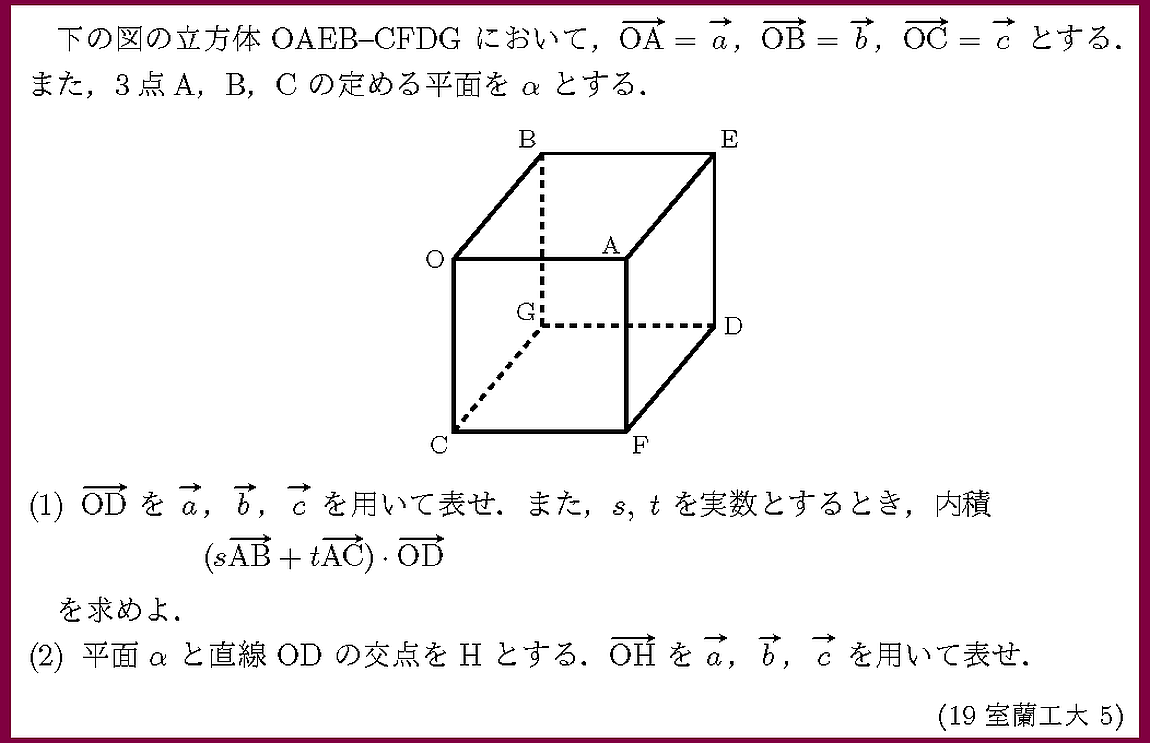
平面と直線の交点を求める問題です．(２)で(１)とヒントとみるか否かで解法が分かれます．
DP＋PEの最小値を求めるにはDの平面αに関する対称点を利用しましょう．その誘導がHです．
このタイプの平面の方程式は，教科書では「発展」として扱われています．
Dから平面ABCに下した垂線の足は線分DEの中点です．
![[PukiWiki]](image/kame.png "[PukiWiki]")
