数学I・Aチェック＆リピート　第5章　§3空間図形　2.多面体

問題文をクリックすると解答をみることができます．

多面体 †

高さは一つの頂点から対面に下した垂線の長さです．

幾何的に処理することも，座標を入れて処理することもできます．

切り口に着目し平面図形として処理していきましょう．

図形をイメージできますか？

オイラーの多面体定理が活躍します．各頂点に集まる辺，面の数に着目しましょう．

図形の対称性に着目しましょう．

接点と中心を含む切り口を考えましょう．

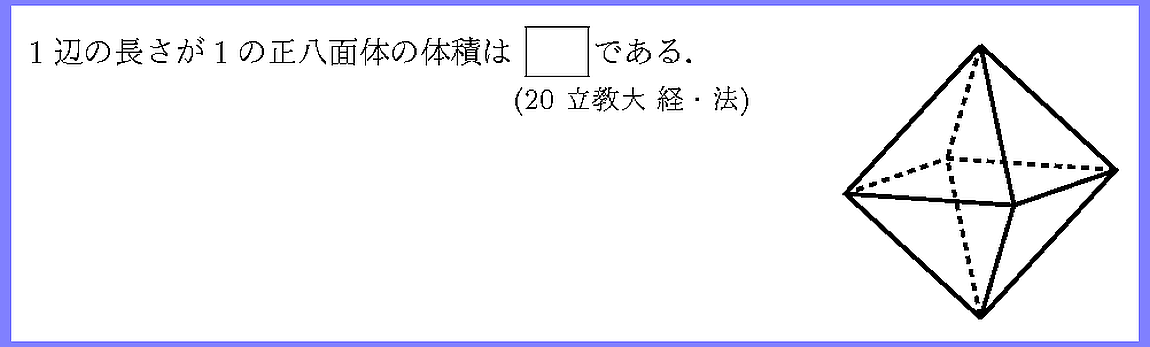
正八面体は2つの正四角錐に分けることができます．

正四面体はすべて相似です．
まずは基本となる正四面体の内接球の半径，高さ，辺の長さをおさえましょう．

幾何的に処理するか，ベクトルで処理するか．

底面の三角形の内接円の直径と高さの比較が必要です．|

(４)のOは四面体の重心です．

四面体の各辺の長さを調べましょう．

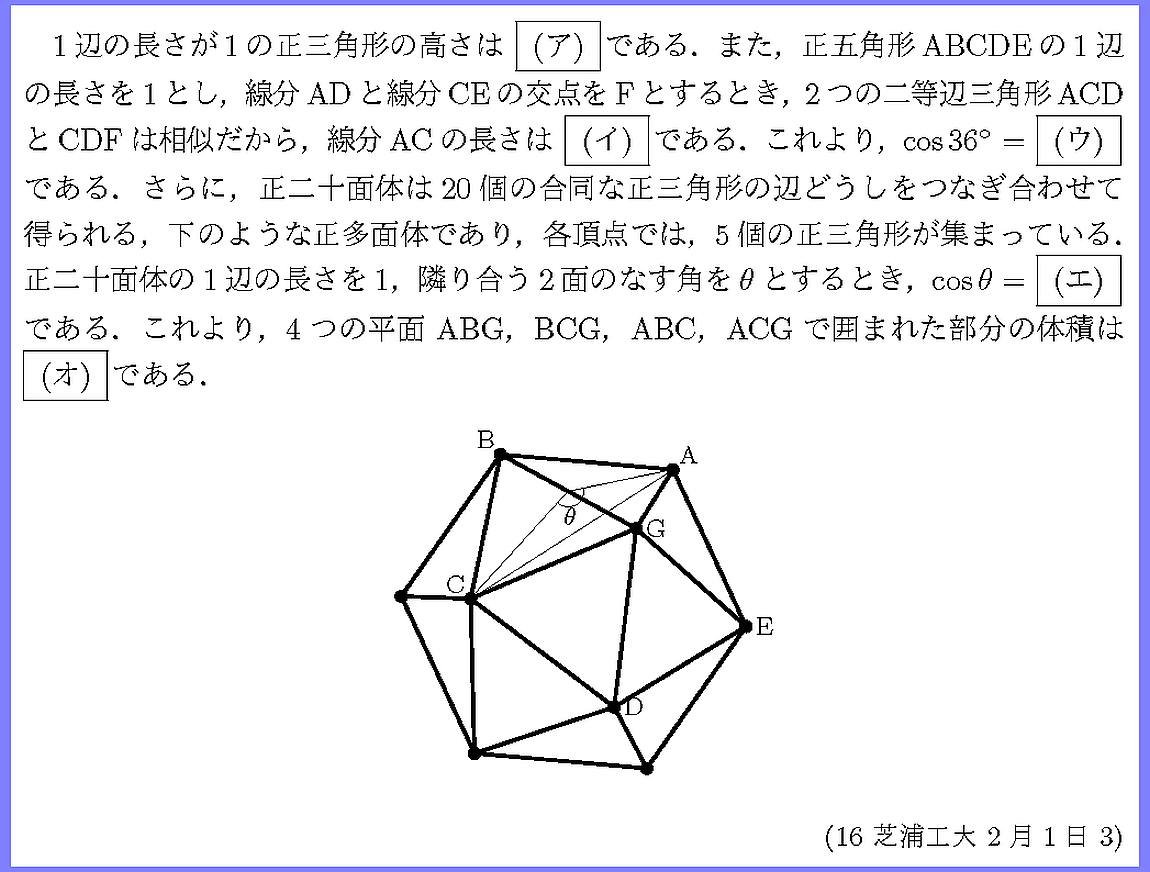
正二十面体を素材に正三角形，正五角形の扱いを確認することができます．