数学I・Aチェック＆リピート
連分数
← n進法 →
第7章 場合の数 ：
集合の要素の個数
問題文をクリックすると解答をみることができます．
n進法 †
類題演習 †
24 共通テスト 本試験 IA 4
ｎ進法を素材に後半は1次不定方程式となっています．
10進法に直して連立方程式を解き，解を2進法で表しましょう．
５進法の定義を思いだしましょう．
10進法に直して差の計算をするか，2進法のままで差の計算をするか．
辺々を10進法で表してみましょう．
7進法で表したときの各位の数の範囲に注意しましょう．
ａ，ｂ，ｃ の範囲に注意しながら値を絞り込みましょう．
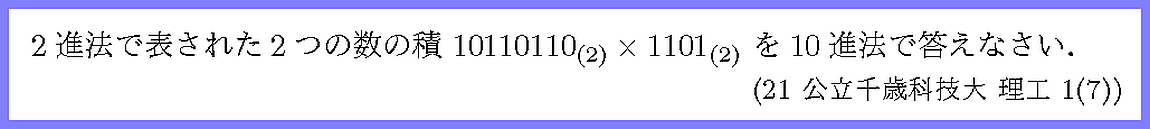
それぞれを10進法に直してから掛け算を実行しましょう．
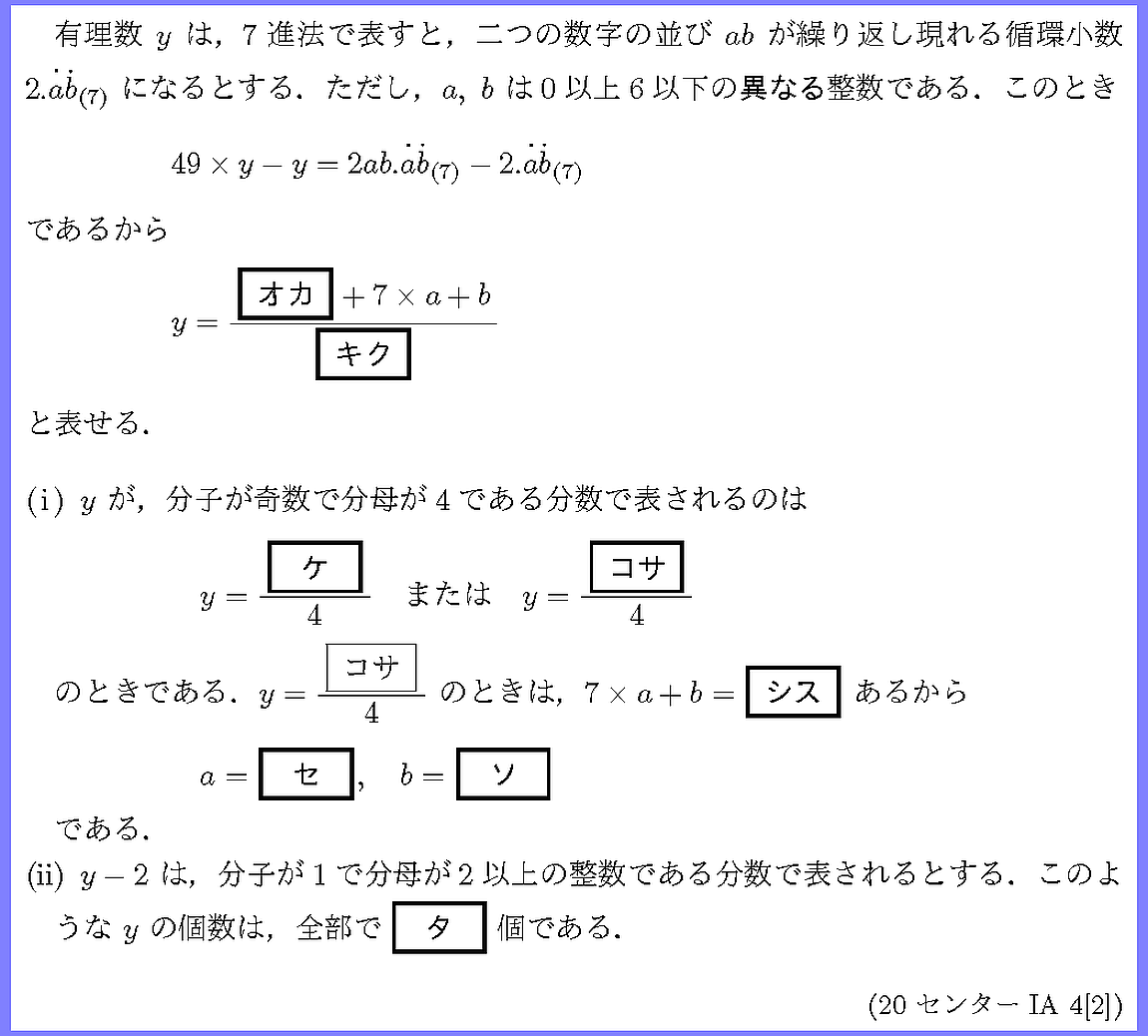
7進法の循環小数から出発して約数・倍数の問題になっています．
7a+b (a≠b) のとり得る値をすべて書き上げてみましょう．
ｎ進法表記の定義を確認しておきましょう．
コンピュータでは2進法での1桁をビット，16進法での1桁(4ビット)をニブルといいます．
したがって，1バイト(8ビット)は16進法で2桁と数となります．
(２)の積は十進法に直して計算しましょう．(３)は値を絞り込んでいきます．
われわれは10進法の計算に慣れています．
7進法で表された数を10進法に直し，
さらにそれを3進法に直せばよいでしょう．
10進法に直して積を計算し，それを7進法に直してもよいのですが，
2数を7進展開して積を計算していくとよいでしょう．
割り算を十進法で行うか七進法で行うか．
２数を１０進法に直して和を計算し，その結果を５進法で表しましょう．
10進法で表された小数を2倍したときの整数部分は2進法の小数第1位の数字です．
類題が19年京都産大にあります．
(1)，(3)はそれぞれ(2)，(4)のヒントになっています．
(4)の和で実力発揮!
ｎ進法についての確認問題です．
2進法→10進法→5進法の書き換えを行います．
(1)で余りの周期性を確認して(2)へと進んでいきます．
余りについては合同式による表記が明快でしょう．
五進法と八進法を十進法でつなぎます．各桁に現れる数字の範囲に注意しましょう．
![[PukiWiki]](image/kame.png "[PukiWiki]")
