数学II・Bチェック＆リピート　第8章　§3空間ベクトル　4.正四面体

数学II・Bチェック＆リピート
球面 ← 正四面体 → 平行六面体，立方体

問題文をクリックすると解答をみることができます．

正四面体 †

類題演習 †

四面体 †

(３)図形の特徴をつかんで体積を計算しましょう．

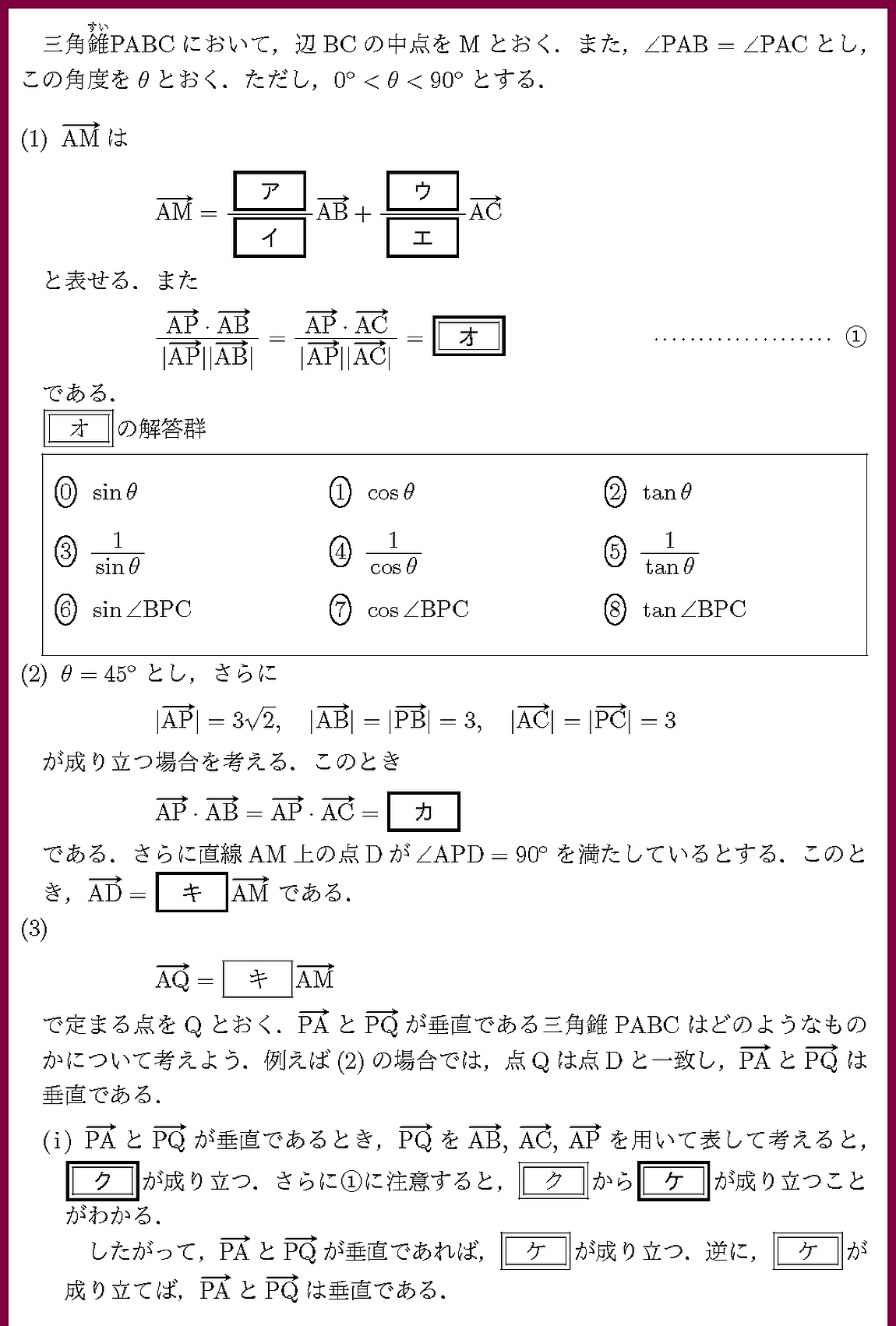
23 共通テスト本試験 IIB 5
最後は誘導にのって進みましょう．

(１)(２)は(３)の準備です．

点が平面にのる条件を確認しておきましょう．

親切な誘導にのって進みましょう．

四面体の中で内積についての計算力が問われています．

空間ベクトルの内積，1次独立について問われています．

(１)はメネラウスの定理を用いましょう．

(4)では四面体ABCDと四面体ABCEの関係を探りましょう．

内積の計算問題です．

分点公式の確認問題です．

四面体を題材に体積比を問うています．分点公式から点の位置を探りましょう．

四面体の重心の存在を問うています．
2本の線分が交わり，残り2本の線分がその交点を通ることを示しましょう．

正四面体 †

四角形PQRSは(２)より平行四辺形であり，(３)もあわせると長方形とわかります．

(2)のLは，(1)の結果と式の対称性を利用して，
L＝(変数)＋(定数)の形まで整理しましょう．

辺の長さによる連立方程式をつくるか，幾何的に考えるか．

正四面体の頂点の位置関係が問われています．

正四面体とは４つ辺の長さが等しい(４つの正三角形からなる)四面体です．

直陵四面体 †

向かい合う線分が垂直なとき，(4)は2本の垂線の交点を求めていますが，
これは4本の垂線でも成り立ちます．
すなわち，Hが四面体の垂心がであることを示しています．

等面四面体 †

等面四面体（4つの面がすべて合同）の外接球の半径を求めています．

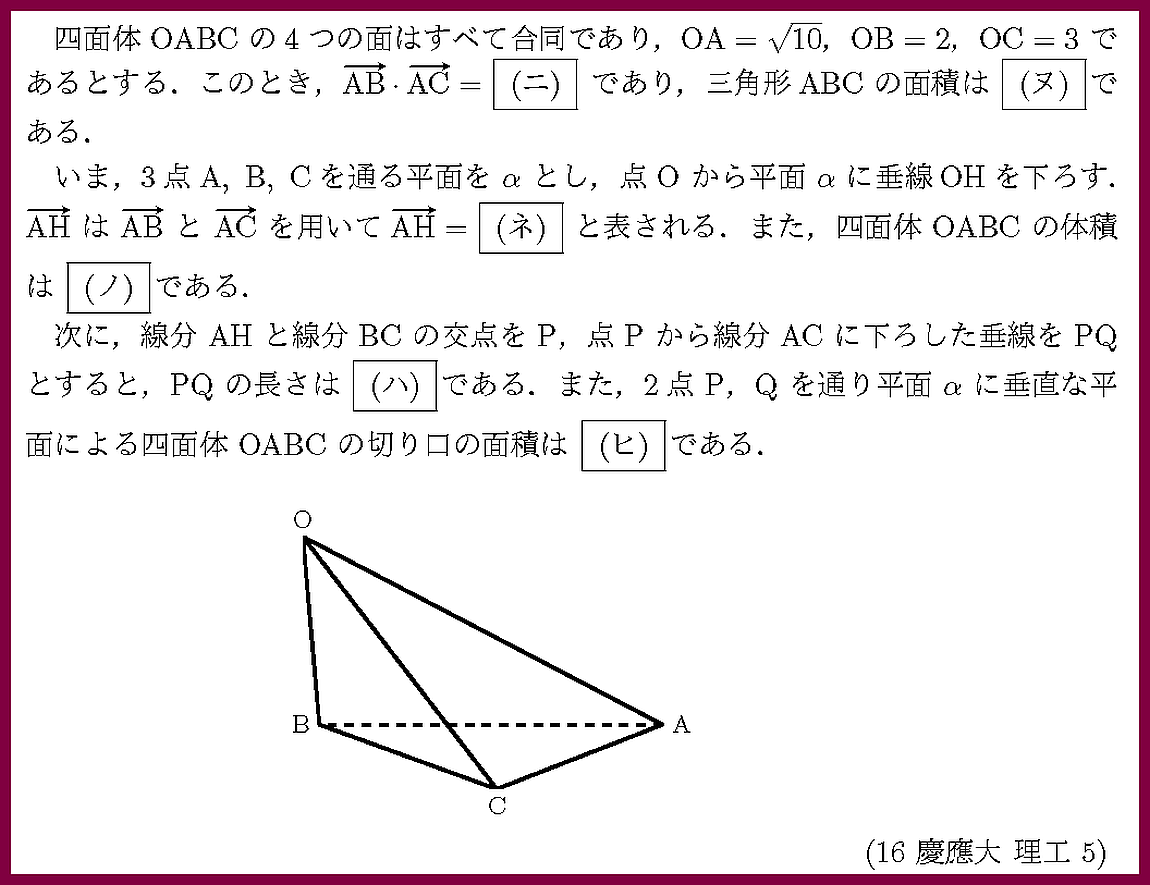
２題分の内容が盛り込まれた問題ですね．図形を把握する力も問われています．