数学I・Aチェック＆リピート　第8章　§3条件つき確率，乗法定理　1.条件つき確率

数学I・Aチェック＆リピート
いろいろな独立試行・反復試行 ← 条件つき確率 → 乗法定理

問題文をクリックすると解答をみることができます．

条件つき確率 †

類題演習 †

持ち点で場合分けして状況を把握しましょう．

(５)(６)が面白い．

23年 共通テスト 追・再試験 IA 3
経路における条件付き確率が問われています．

条件付き確率の定義を確認しておきましょう．

(１)(２)(３)が無駄なく(４)につながっています．

最大確率，条件付き確率と盛沢山です．

円順列を舞台に条件付き確率が問われています．
隣り合うものは一つとみなす，隣り合わない並べ方は2段階操作で実現させる
といった操作を思い出しましょう．

(２)(３)では取り出すカードの文字が決まっているところから順に数えるとよいでしょう．

条件を満たす目の出方をおさえましょう．

長い文章です．事象を設定しながら状況を読み取りましょう．

(１)はどの袋から玉を取り出すかで場合分けしましょう．

条件付き確率が問われています．事象を設定して，題意を明確にしましょう．

(１)(２)(３)は(４)への親切な誘導です．

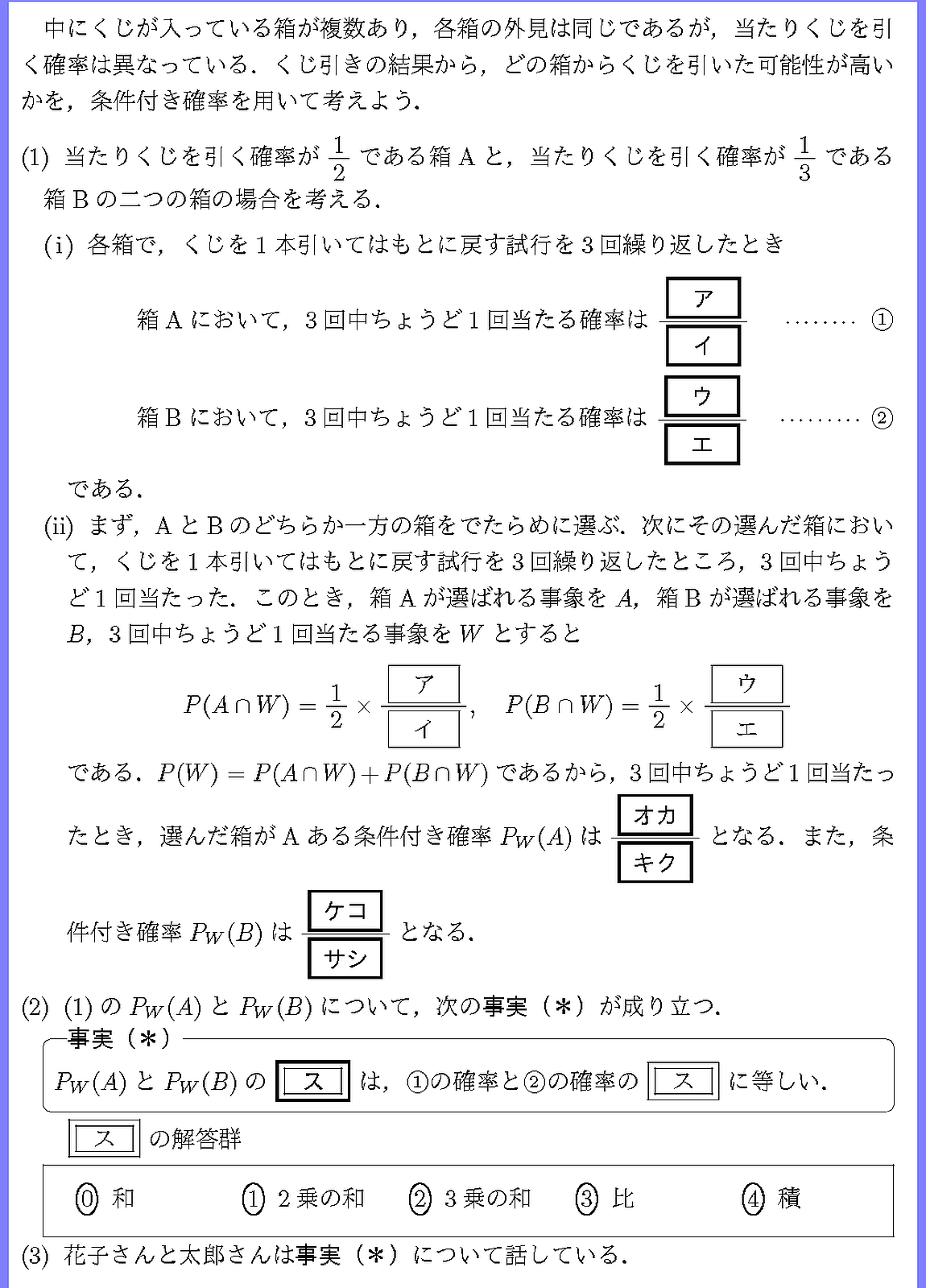
21年 共通テスト IA 3
どの箱からくじを引いた可能性が高いかを問うています．
会話文の誘導にのりましょう．

(２)(ii)は条件付き確率での余事象を考えましょう．

10枚のカードはすべて区別します．(２)は(３)のヒントです．

(１)表を利用します．(３)(４)条件付き確率に慣れましょう．

２つのサイコロの出た目の差の絶対値を表にしましょう．

(1)は(3)のヒントになっています．

6枚のカードをすべて区別して横1列に並べてみましょう．

3で割った余りの和で状況を表現しましょう．

(1)，(2)は頻出問題です．
(3)では(2)の利用を考えましょう．

(１)(２)は(３)(４)の条件付き確率の準備です．
(３)(４)は条件を満たす状況を時間の流れに沿って拾い上げていきましょう．

ｎが偶数であるか奇数であるかの場合分けが必要です．

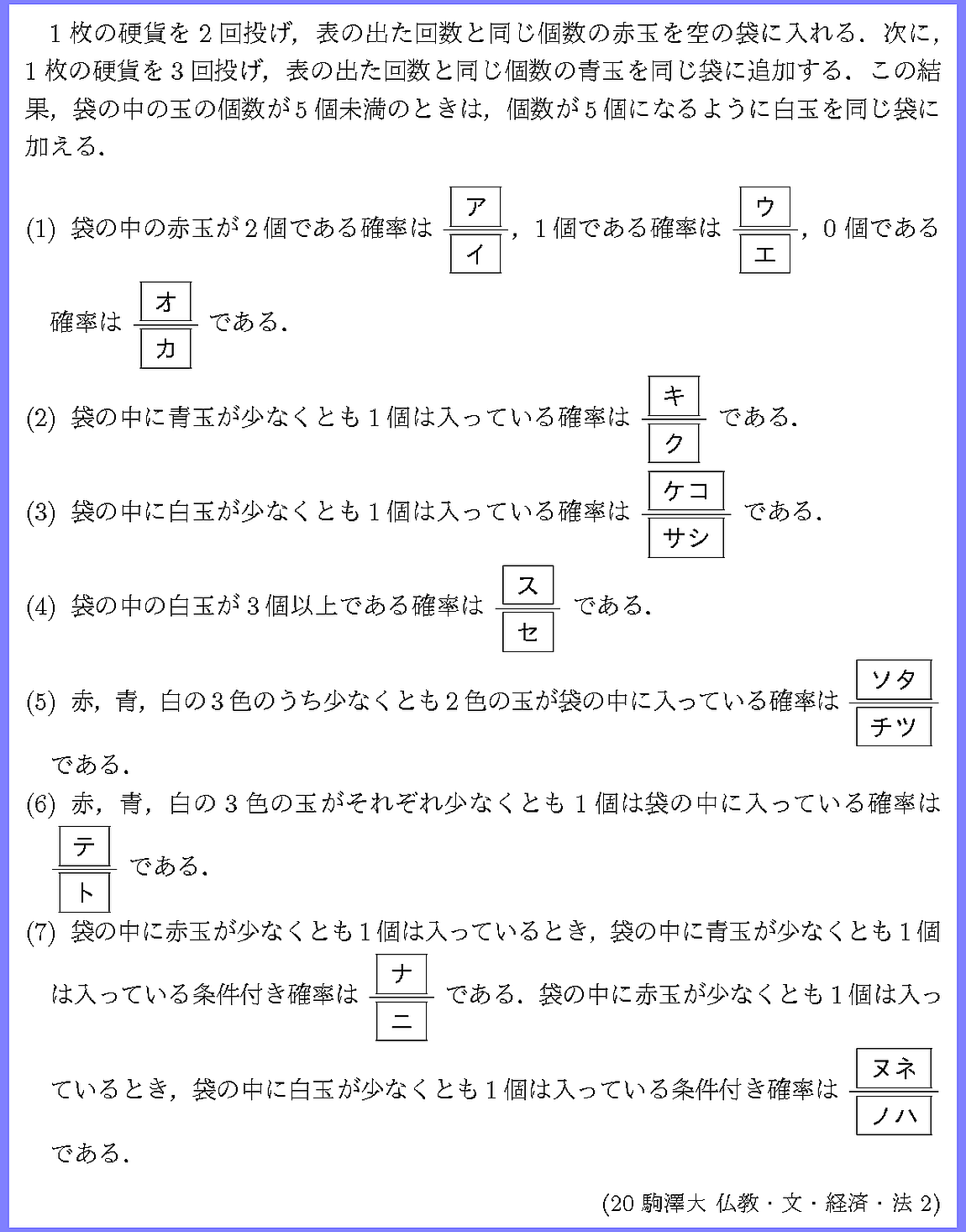
設問7個は多いですね．
(5)，(6)，(7)での「少なくとも〜」の扱いに慣れましょう．

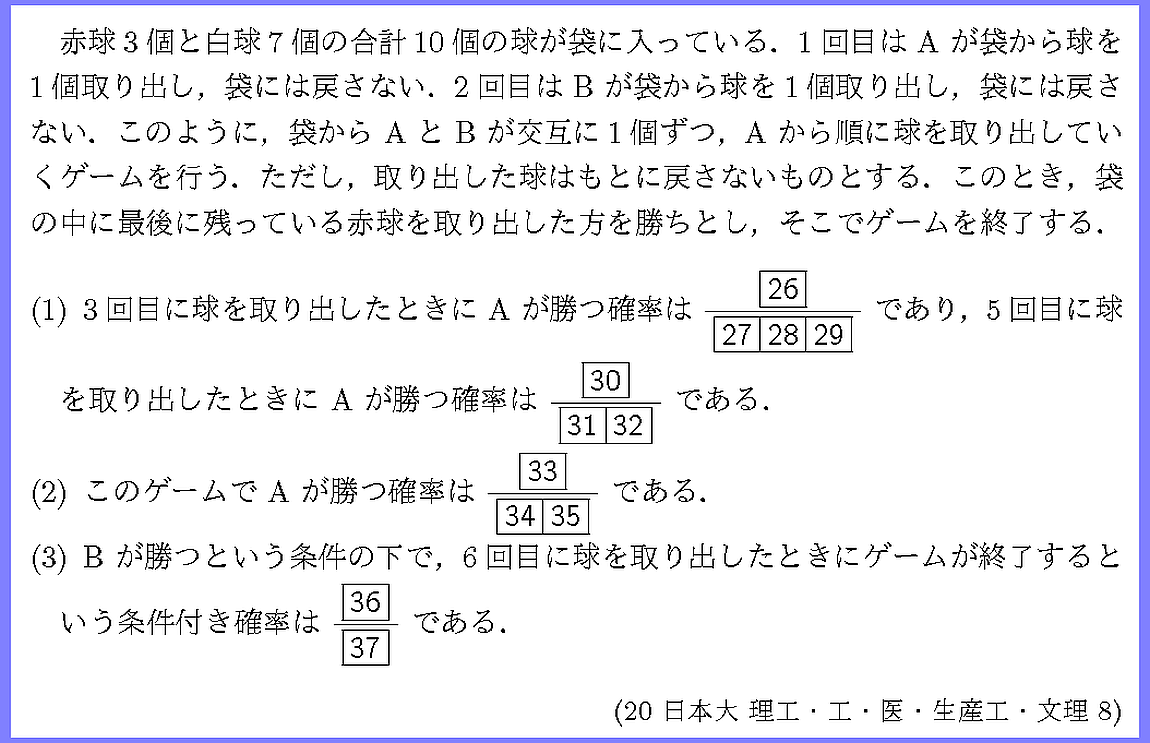
非復元事象の確率であり，くじ引きのときと同じように，
球を横一列に並べること置き換えて考えることができます．

条件付き確率の基本問題です．

(1)は乗法定理と条件付き確率の確認問題です．
(2)確率の増減は隣り合う項の比と1との大小比較で決まります．

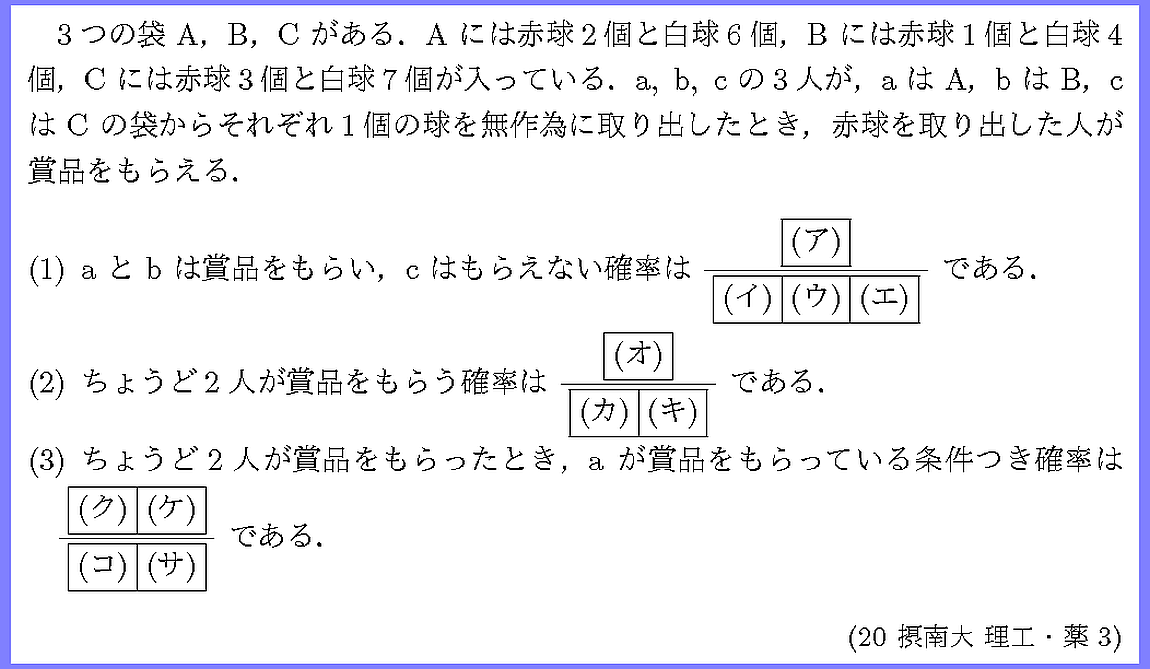
3人の球の取り出し方は独立です．
(1)，(2)は条件付き確率(3)の準備となっています．

確率の計算の基本を問うています．

(3)は条件付き確率であり，(1)は(3)の準備になっています．
(2)は直接計算するか，余事象を考えるかに分かれます．

条件をみたす場合の数を求めます．
(1)は重複組合せを利用することもできます．

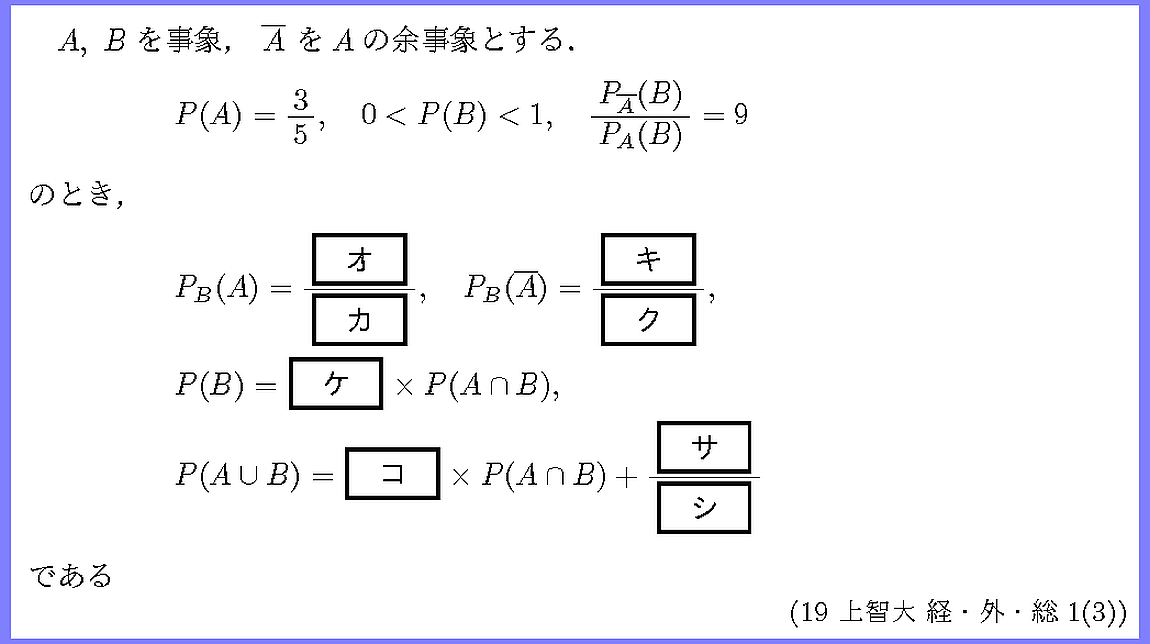
条件付き確率と加法定理を絡めた確率の計算問題です．

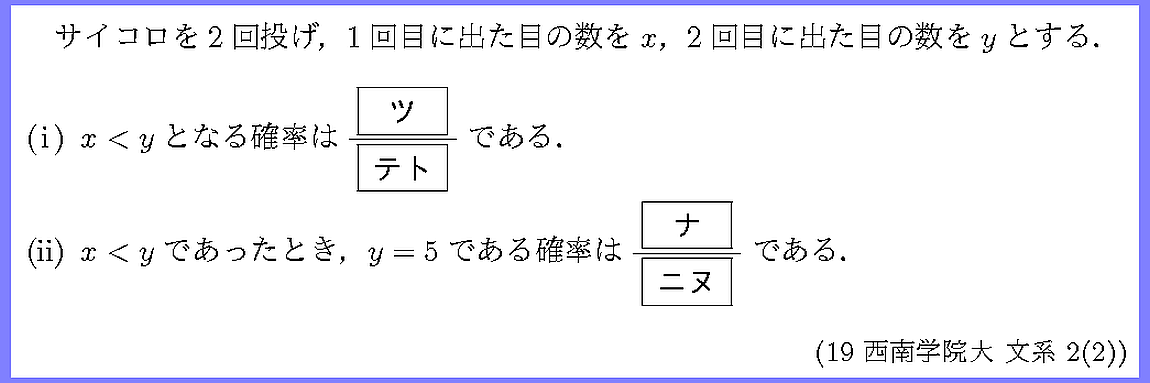
サイコロを2回投げるときの目の出方を表にすると一気に解くことができます．

a，b，cが三角形の3辺の長さとなる条件は，「|b-c|<a<b+c」であり，
a≧b≧c>0のときは「a<b+c」です．

異なる玉9個の順列を考えるとよいでしょう．

条件付き確率の基本問題です．

条件付き確率の基本問題です．
時間の流れにしたがって確率を計算していきましょう．

事象を設定し条件付き確率を式で表しましょう．

(2)は解法が分かれそうです．

余事象の確率，加法定理，条件付き確率といった確率の基本定理の理解を問うています．

(1)，(2)ではAの取り出した2個の玉の色により袋の中の玉がどう変わるかに注意します．
この結果が(3)の条件付き確率で活きてきます．