数学IIIチェック＆リピート　第2章　§2複素数平面　7．円の方程式

問題文をクリックすると解答をみることができます．

円の方程式 †

(１)は数学的帰納法，(２)は三角不等式が使えます．

円と垂直二等分線について問われています．
(３)では回転，重心も登場しいろいろな知識が問われています．

(３)では２つの円の共有点の位置関係を捉えましょう．

複素数平面上の円と直線を扱えるようにしましょう．

(１)は極形式，(２)は直線ｌの動く範囲を問うています．

複素数平面上で外接円に絡んで双曲線が登場してきます．

アポロ二ウスの円と垂直二等分線が登場しています．

アポロ二ウスの円と呼ばれています．

Pが描く円はアポロ二ウスの円と呼ばれています．

（２）αとβは共役の関係にあり，中心を表すγは実数です．
（３）直角となる頂点は確定されます．

２円が２点を共有する条件が問われています．

(１)はアポロ二ウスの円と呼ばれています．
(２)ｚが存在するためのｗの条件を求めるか，ｚ→ｗの変換の意味を考えるか．
(３)２円が内接するための条件は (中心間の距離)=(半径の差) です．

4点が同一円周上にあるための条件(共円条件)

アポロ二ウスの円が問われています．

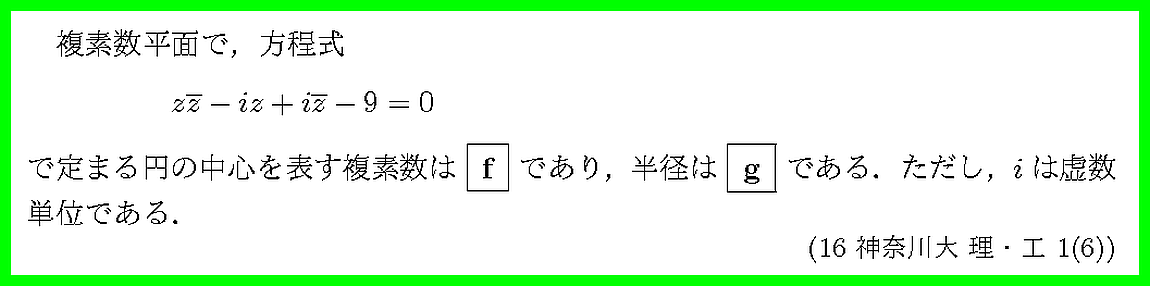
中心，半径がわかる形に式を変形しましょう．

(2)(3)は，3点が単位円上にあるとき，第4の点がこの円上にあるための必要十分な条件を求めています．