数学I・Aチェック＆リピート　第6章　§3整数の性質　1.倍数・約数

数学I・Aチェック＆リピート
多面体 ← 第6章　整数 ： 倍数・約数 → 最大公約数，最小公倍数

問題文をクリックすると解答をみることができます．

倍数・約数 †

類題演習 †

約数 †

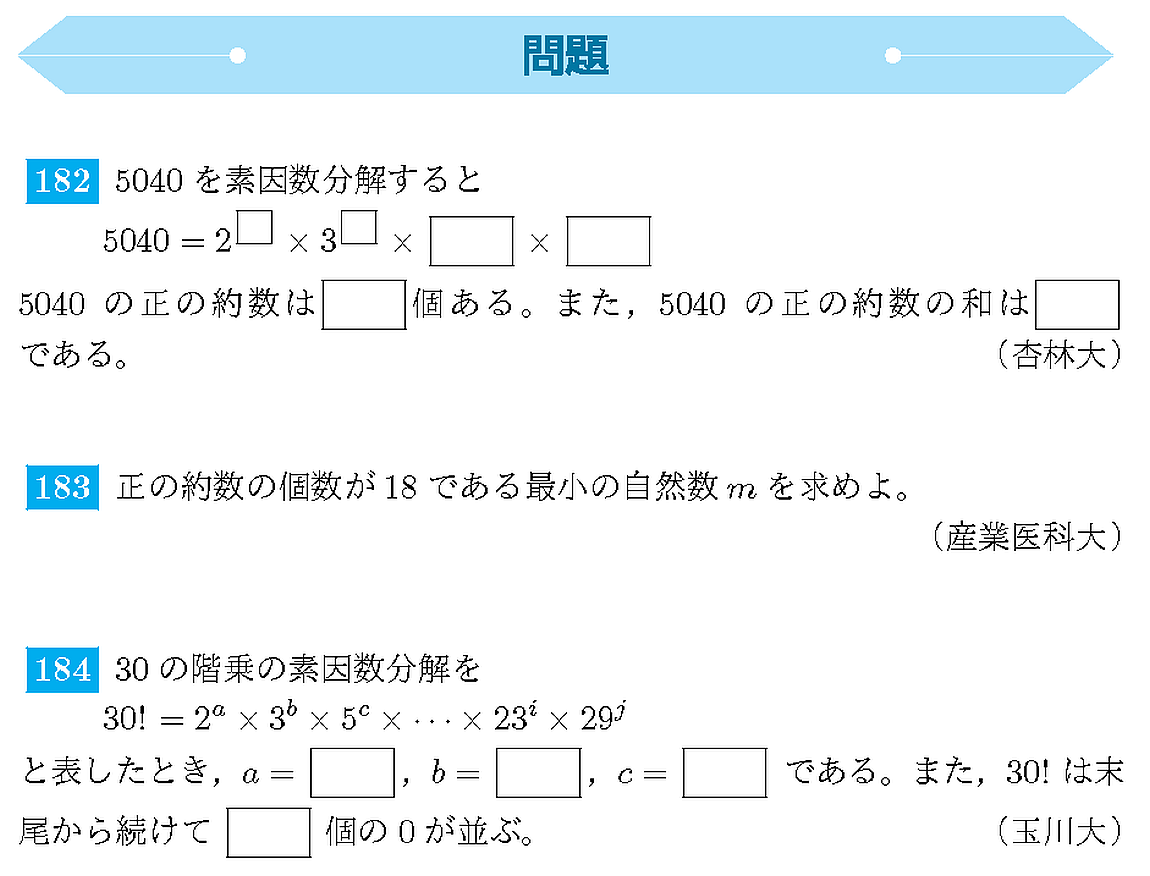
約数の個数と総和について確認しておきましょう．

左辺の因数分解，右辺の素因数分解から始めましょう．

ｆ(ｎ)はオイラーのトーシェント関数(略してオイラー関数)と呼ばれています．

約数の総和について問われています．

まずは素因数分解しましょう．

求める最大のｍとは，54!に含まれる素因数3の個数のことです．

約数の個数，総和についての基本問題です．

20220を素因数分解します．
途中，まだ分解できるか否かで悩まされることもあります．
例えば337は素数ですか？合成数ですか？

まずは素因数分解しましょう．

整数を素因数分解したときの約数のあり方を絞っていきましょう．

倍数 †

９の倍数である条件が問われています．

まずはｍの範囲を絞りましょう．

連続した3整数の積は6の倍数です．

6の倍数，8の倍数，24の倍数．(3)では対偶を考えましょう．

連続した3整数の積をつくるか，3で割った余りで場合分けして調べるかでしょう．

連続したｋ個の整数の積はｋの倍数であることを利用しましょう．

「504」 を素因数分解することにより，n の因数が絞られます．

連続した３つの整数の積は６の倍数です．

(３)は二項定理を利用することもできます．

ｆ(ｎ)の分子は連続した４整数の積です．必ず含まれる約数に着目しましょう．

(1)は11の倍数であるための必要十分条件です．
(2) (Nの5乗)−N が5の倍数であることを示すことになります．
連続した5整数の積が現れるとうれしいのですが…．

(１)は自然数ｎについての命題です．数学的帰納法を用いましょう．

素数 †

証明の糸口が問われています．

素因数分解をテーマにしたきれいな問題ですね．

(２)はカタラン数と呼ばれるものです．
(３)「すべて求めよ．」とあるので，ｎの範囲は絞れるはずで，
大きなｎは範囲から外れるはずです．

(１)ｋ＝２，３，５，７，11，…と素数を代入してみると様子が見えてきます．
(２)は(３)のヒントでしょう．(３)は(２)を無視して背理法を用いることも可能です．

a^n-b^n の因数分解と対偶を使います．

ｐが小さいときは具体的に ｐ^4+14 を計算できますが，いつまでもこれを続けることはできません．
ｐ^4+14 は素数でないことを示すのだから，ｐがある程度大きくなったときには，
ｐ^4+14 が２で割り切れないか，３で割り切れないか，…と考えてみましょう．

(１)分母分子の因数1個ずつのペアを考え，ｎ≧ｋ＋２を利用しましょう．
(１)は(２)のヒントです．

右辺は因数分解できます．

種々の問題 †

(1)は(3)のヒント．
(2)はｎを3で割った余りで分類しながらすべての場合を議論しましょう．
(3)はf(n)を素因数分解したときの因数のあり方を調べましょう．

(1)は(3)のヒント．
(2)はｎを3で割った余りで分類しながらすべての場合を議論しましょう．
(3)はf(n)を素因数分解したときの約数のあり方を絞っていきましょう．

(3)までは基本問題です．(4)はコツコツ数えていきましょう．

互いに素をテーマにした問題です．
(2)まで標準．(3)(4)の論証は差がつきます．

1からNまでの整数のうちpの倍数であるものの個数はN/pの整数部分(Nをpで割ったときの商)ですが，
これを[N](ガウス記号)と表すことにしましょう．

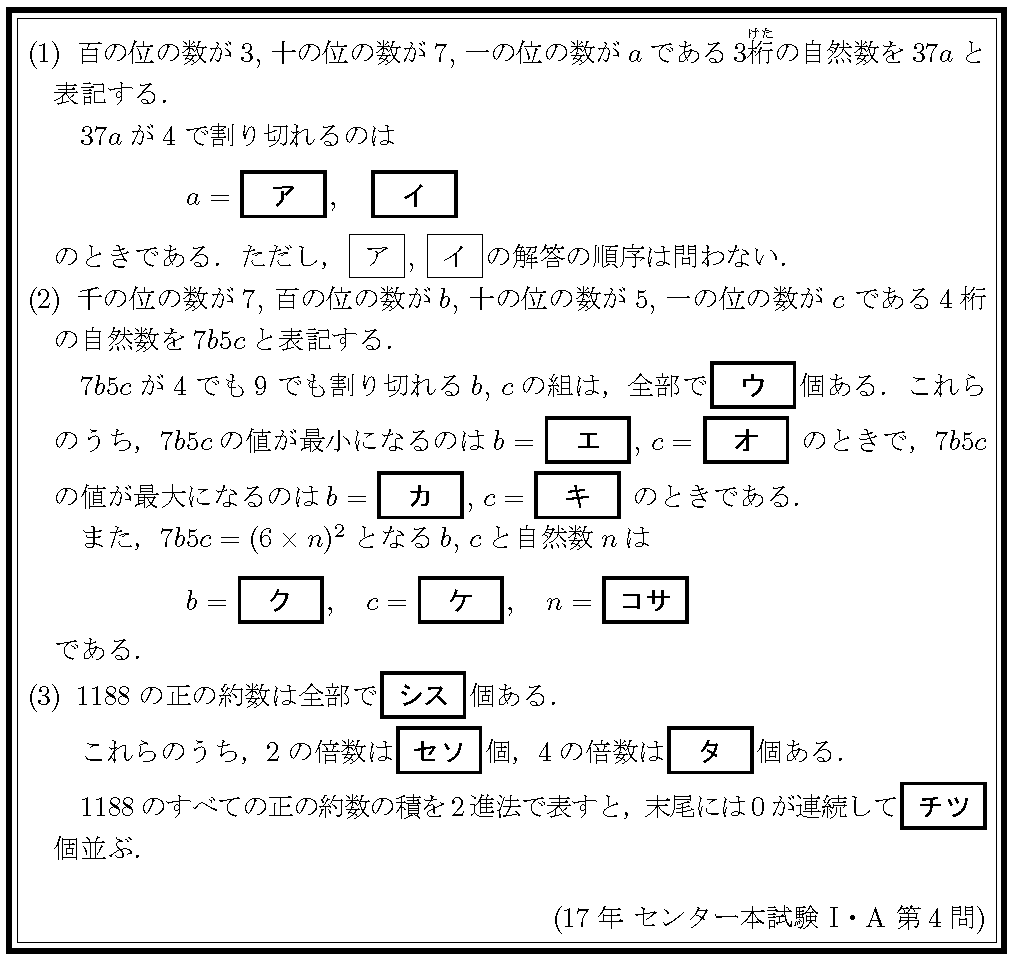
(1)は公式として覚えている人もいるでしょう．
(2)は(1)の応用です．