数学IIIチェック＆リピート　第5章　§1積分の計算　10．定積分で表された関数

数学IIIチェック＆リピート
無理関数の積分 ← 定積分で表された関数 → 定積分と漸化式

問題文をクリックすると解答をみることができます．

定積分で表された関数 †

類題演習 †

tの値の範囲で場合分けして絶対値をはずことから始めましょう．

定積分で表された関数の極限が問われています．微分係数を確認しておきましょう．

(3)f'(x)の符号の変化に着目します．

最小となるaの値を求めるだけなら，g(a)と微分すればよいのですが，
最小値も求めるので積分は避けられません．

定積分で表された関数を用いて微分の基本が問われています．

積分変数はｔです．(２)では場合分けして絶対値をはずします．

積分部分は定数です．

ｆ(ｘ)における積分部分は定数です．

微分積分の基本的な計算力が試されています．

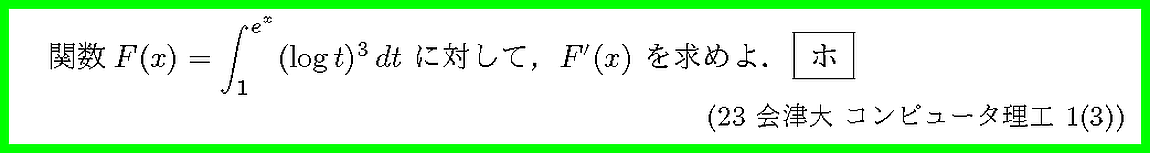
微分と積分の関係が問われています．

最大・最小となるｘを求めるには，積分してから微分するか，直接微分するかで別れますが，
最大値・最小値を求めるときの積分計算は避けられません．

微分することと初期条件f(a)=0を用います．

絶対値をはずすためにｘの範囲を場合分けしましょう．

(１)の微分方程式の解くための誘導が(２)，(３)の設問となっています．

まずは微分し，最小となるｘの値を探りましょう．

加法定理を用いて，被積分関数を展開し，ｘは積分の外に出してしまいましょう．

ｆ(x)は x≧0，x≦0 で場合分けされて確定します．
ｇ(x) は積分区間 x-1≦ t≦ x に 0 が含まれるか否かで場合分けすることにより決まります．

積分変数はｔです．積分内のｘを積分の外に出しましょう．

定積分で表された関数の典型問題です．
(1)(2)(3)は(4)で必要な計算の準備です．

与えられた関数はｘについての２次関数です．