数学I・Aチェック＆リピート　第8章　§3条件つき確率，乗法定理　2.乗法定理

数学I・Aチェック＆リピート
条件つき確率 ← 乗法定理 → 原因の確率

問題文をクリックすると解答をみることができます．

乗法定理 †

類題演習 †

25 共通テスト 本試験 旧IA 3
二人，三人によるじゃんけんの確率をすべて求めましょう．

(b)(c)は起こりうる状況をすべて拾い上げましょう．

(2)では条件(b)に注意しましょう．

「かつ」の確率は乗法定理を用います．

非復元事象であることに注意しましょう．
(2)は(3)の準備になっていますが，(3)での場合分けは多いです．要領よく正確に計算しましょう．

いろいろな解き方ができます．

すべての状況を考えてみましょう．

玉の取り出し方を把握しましょう．

球の並べ方におきかえて考えましょう．

状況の変化に注意して確率を計算しましょう．(４)は(５)のヒントです．

球の移動を把握しましょう．

球の移動の状態をすべて書き上げましょう．

(２)は球の取り出し方を把握しましょう．

多人数でのあいこの確率は余事象を考えるとよいでしょう．

状況の変化をとらえましょう．

取り出したカードを「戻す」，「戻さない」それぞれの確率が問われています．

状況を把握できるか，また状況に応じた確率の計算ができるかを問うています．

(1)，(2)は乗法定理を用います．
また，これらは(3)のヒントになっています．

袋Aにある玉の個数の推移を把握しましょう．

硬貨投げの結果により球の取り出し方は変わります．

(3)の設問は違和感があります．
確率においては赤球3個は区別しますが， 並べ方では色の配列を問うていて赤球3個は区別しません．
他の色でも同じです．

くじ引きの基本問題です．
「同様に確からしい」を保証するためにくじはすべて区別します．

（１）（２）確率の最大値を求める基本問題です．
（３）袋Aからの球の取り出し方は2通りあります．

変化の様子を把握しましょう．

状況の変化を把握しましょう．

乗法定理を用います．

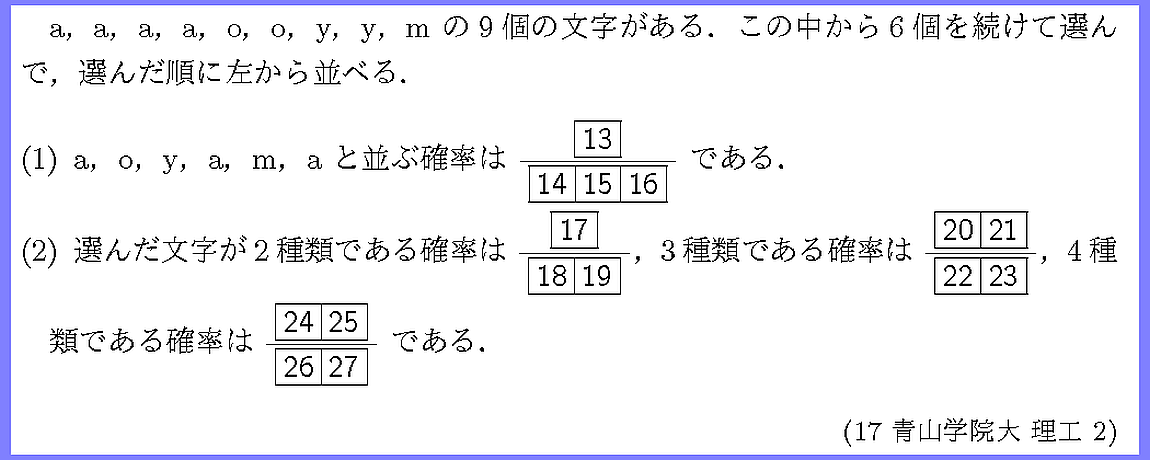
確率ですから，文字の選び方は等確率な選択となります．
すなわち，9文字をa_1，a_2，…，y_1，y_2，m といった具合にすべて区別します．

10枚のカードはすべて区別します．例えば，1，1，4の順に数字が並ぶカードの取り出し方は，
2つずつある１，4を１，1'，4，4'と区別すると11'4，11'4'，1'14，1'14'の4通りがあります．

ポリアの壺と呼ばれる有名問題です．