数学I・Aチェック＆リピート
2つの放物線の共有点
← 絶対値のついた2次関数のグラフ →
1次関数の最大・最小
問題文をクリックすると解答をみることができます．
絶対値のついた2次関数のグラフ †
類題演習 †
24 共通テスト 追・再試験 IA2-1・I3-2
絶対値がついた２次関数のグラフが問われています．それにしても長い問題文ですね．
(2)グラフを描いてみましょう．
y=x|x+3| のグラフと y=k のグラフの共有点を考えましょう．
定数pを分離して考えるとよいでしょう．
７/３≦ｘ≦20/３の範囲で共有点をもつか否かなど細かい配慮も必要です．
5-1problem.png "問題文をクリックしてみて下さい．")
実数解の個数は２つのグラフの共有点の個数と一致します．
絶対値のついた２次関数のグラフについての基本問題です．
２次式|=x+m とみるか |２次式|-x=m とみるかに分かれるでしょう．
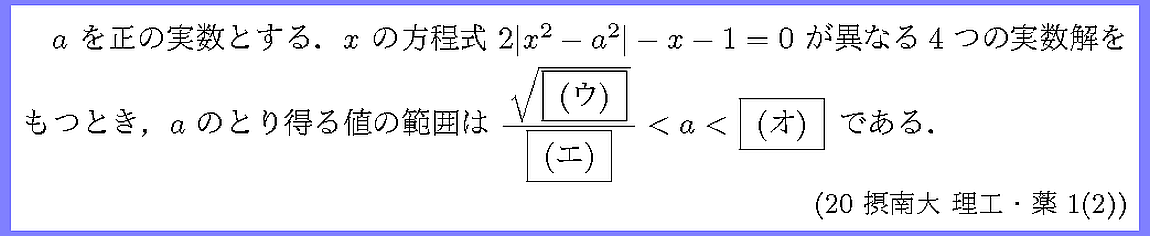
グラフの利用を考えましょう．
|f(x)|=c の実数解は y=|f(x)| と y=c のグラフの共有点のｘ座標です．
グラフの折れ目，頂点とｘ軸の位置関係に着目してｍの値で場合分けしましょう．
ｙ＝ｆ(ｘ）とｙ＝ｘ＋ｋの共有点の個数は，f(ｘ)＝ｘ＋ｋ，すなわち
ｆ(ｘ)−ｘ＝ｋの実数解の個数と一致します．
![[PukiWiki]](image/kame.png "[PukiWiki]")
