数学I・Aチェック＆リピート
合同式
← 不定方程式（1次） →
不定方程式（2次以上）
問題文をクリックすると解答をみることができます．
不定方程式（1次） †
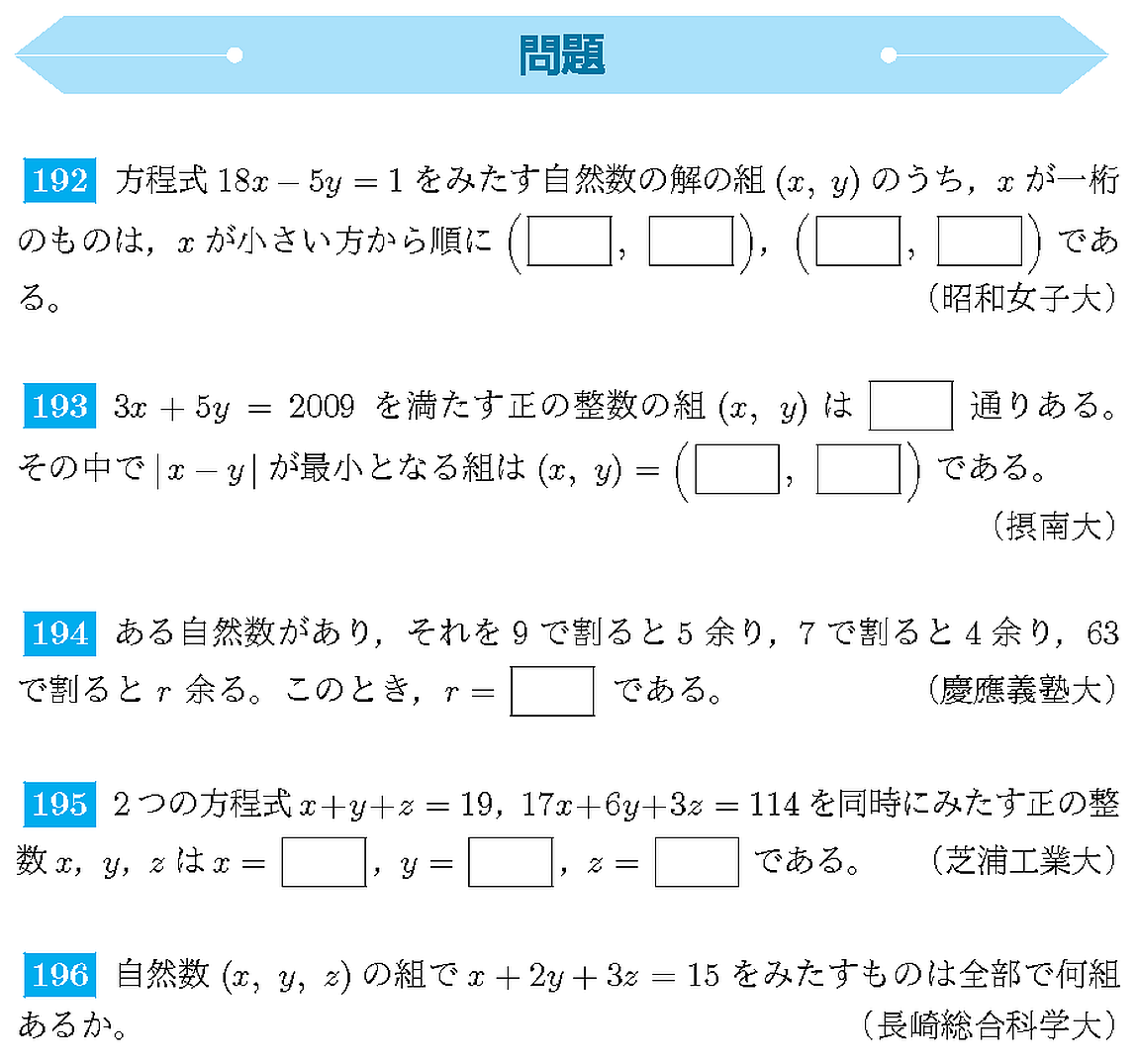
類題演習 †
23共通テスト追・再試験IA4
３元１次不定方程式の登場です．誘導があるとはいえ解の存在条件と問うのはキツイのでは．
ユークリッドの互除法を用いて1次不定方程式を解いています．
(１)(２)ともに１次不定方程式の特殊解を探します．
特殊解を見つけることから始めます．
(１)は(２)のヒントです．(２)は与えられた数を23の2乗で割ることから始めましょう．
特殊解はユークリッドの互除法を利用しましょう．
(３)では｜xy-2023｜≧０なので，｜xy-2023｜=０となるｘ，ｙは存在するか，
｜xy-2023｜=１となるｘ，ｙは存在するか……と考えます．
ユークリッドの互除法を用いましょう．
３ｍ+５ｎ=ｌを満たす自然数の組(ｍ，ｎ)が存在するか否かが問われています．
誘導にのりながら進んでいきましょう．
整数と数列の融合問題です．与えられた条件から1次の不定方程式をつくることができます．
1次不定方程式を解くだけではなく，解の存在条件も問うています．
(１)の1次不定方程式は教科書レベル．
(２)で原点と直線上の格子点との距離が加わりますが，
入試問題としては基本レベルでしょう．
629と481の最大公約数で辺々を割って簡単な1次不定方程式に変形します．
互除法を用いて，１次不定方程式の特殊解を求めます．
与えられた条件から1次不定方程式が導かれます．
与えられた条件から1次不定方程式が導かれます．
与えられた条件から1次不定方程式が導かれます．
与えられた条件から1次不定方程式が導かれます．
1次不定方程式の典型問題です．
まずは特殊解をみつけましょう．
与えられた条件から1次不定方程式が導かれます．
まずは解の組を一つを求めましょう．
互除法を用いるとよいでしょう．
(1)は1次不定方程式の基本問題です．
(2)は背理法を用いましょう．
1次の不定方程式を解く問題です．
(4)を満たす整数の存在は「中国の剰余定理」として一般化されています．
1次の不定方程式の基本です．
1次不定方程式の特殊解は互除法を利用して求めましょう．
(2)(3)の流れは1次不定方程式の典型的な解法になっています．
互除法により2つの数の最大公約数が求められること，
および互除法を逆にたどることにより1次不定方程式の解が得られることを確認しています．
どちらも整数を扱うときの基本事項です．
使えるだけでなく，なぜか？という姿勢で問題に取りくむことも大切です．
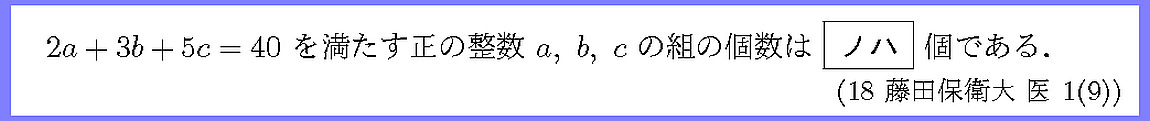
3元の1次不定方程式です．
40は大きな値ではないので正の数a,b,cに値を代入しながら解くこともできますが，
一般化も視野に入れた解法を心掛けましょう．
3元の1次不定方程式です．
2元のときと同じようにして一般項を求めることができます．
一般項を求めてから，ｘとyの平方和の最小値を求めましょう．
![[PukiWiki]](image/kame.png "[PukiWiki]")
