オイラー関数

FrontPage

オイラーの 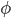$\phi$ 関数 †

ｎを正整数とするとき，１からｎまでの整数で，ｎと互いに素となるものの個数をφ（ｎ）と表す．
整数ｎとａとが互いに素とは，それらの最大公約数が１となることでもある．
m，nが互いに素であるとき
$\phi(mn)=\phi(m)\phi(n)$
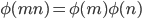
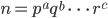$n=p^aq^b\ \cdots\ r^c$ (p，q，…，rは素数a，b，… ，cは自然数) のとき
$\phi(n)=n \left(1-\frac{1}{p}\right)\left(1-\frac{1}{q}\right)\cdots\left(1-\frac{1}{r}\right)$

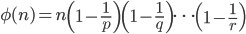
オイラーの定理 ｎを正整数，ａをｎと互いに素な整数とする．このとき
$a^{\phi(n)} \equiv 1 \pmod n$
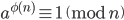
が成立する．

n=p(素数のとき)，φ（ｐ）＝ｐ－１であるから
$a^{p-1} \equiv 1 \pmod p$
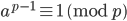
が成立する．これはフェルマーの小定理とよばれている．

↑

参考 †

オイラー関数(kamelink) / wikipedia / 青空学園　/ オイラー関数とオイラーの定理 / kyの書架

↑

入試問題 †

問題文をクリックすると解答をみることができます．

(1)pのn乗以下の自然数からpのn乗と互いに素でないものを除きましょう．
(2)背理法を用いましょう．与えられた条件はhと互いに素なh未満の自然数は6個以下ということです．
(3)は2と3はhと互いに素でないことに着目します．すなわち，2と3はhの素因数です．
φ(mn)=φ(m)φ(n)については「ここ」を参照してください．