数学IIIチェック＆リピート　第5章　§2積分法の応用　3．パラメータ表示された曲線と面積

問題文をクリックすると解答をみることができます．

パラメータ表示された曲線と面積 †

(２)でもｔで積分計算をおこないます．

ｔによる積分計算を行います．

(２)はQの軌跡を描くための準備です．最後の面積はキレイな値です．

パラメータ表示された曲線(サイクロイド)について接線，面積が問われています．

(３)では曲線とｘ軸で囲まれた図形を明記(グラフでなくてもよい)して面積の計算に入りましょう．

(3)ではCの概形を描いてみましょう．

極座標表示された曲線をｘ，ｙのパラメータ表示に直しましょう．
(５)の面積はｙ軸に沿った積分を考え，θによる積分に置き換えましょう．

方針で戸惑うことはないでしょう．計算力が問われています．

どの部分の面積を計算するのかを明記しましょう．

パラメータ表示された曲線の面積計算です．

媒介変数表示された曲線での面積・体積を問うています．

Kはルーローの三角形と呼ばれている図形です．

(１)，(２)はPの軌跡を描くための誘導です．
(３)通過領域にはOPの最大値を半径とする四分の一円が現れます．

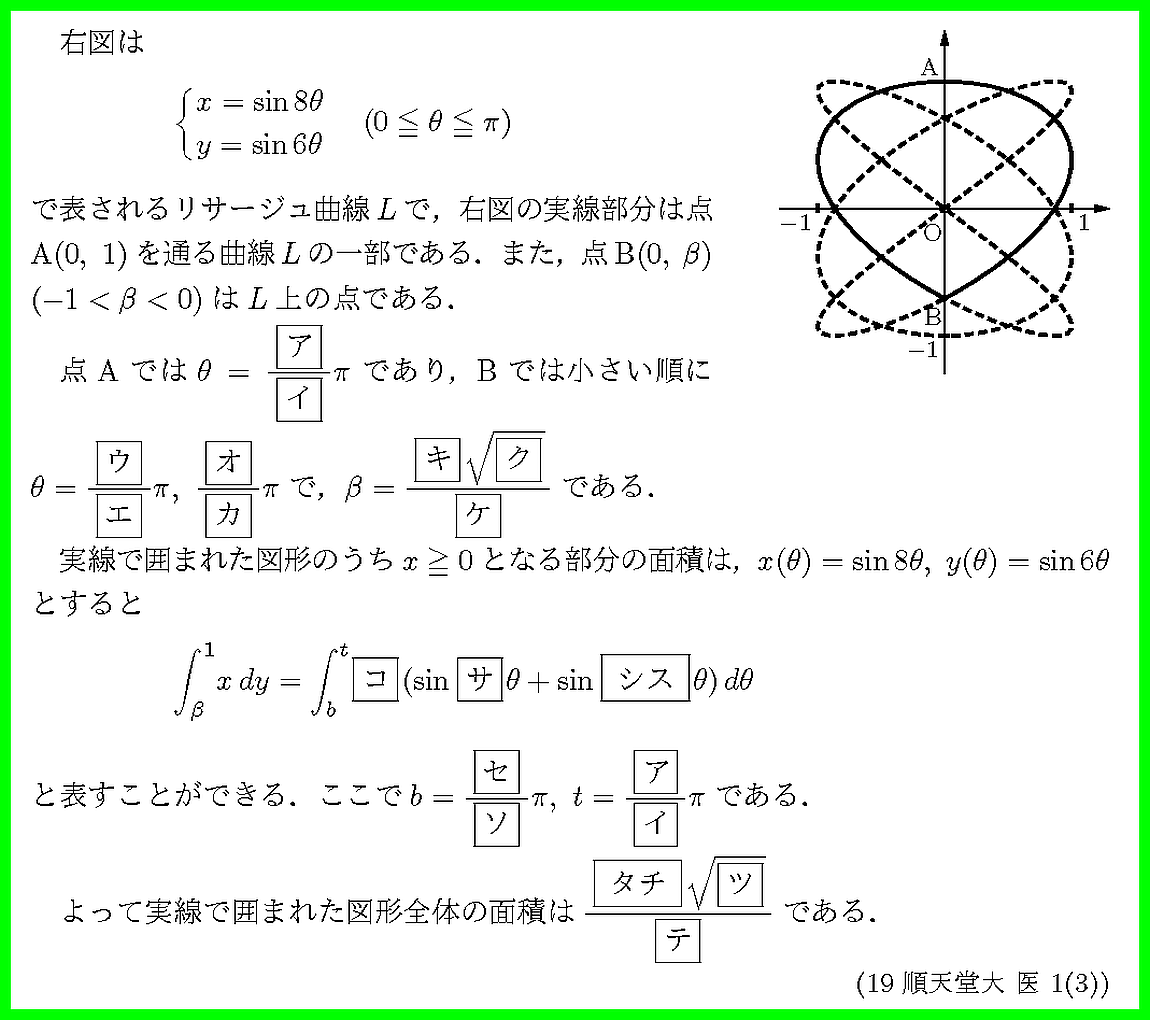
A，Bはy軸上の点です．θの値の候補を絞りましょう．

y=f(x)のグラフは，単位円の伸開線です．

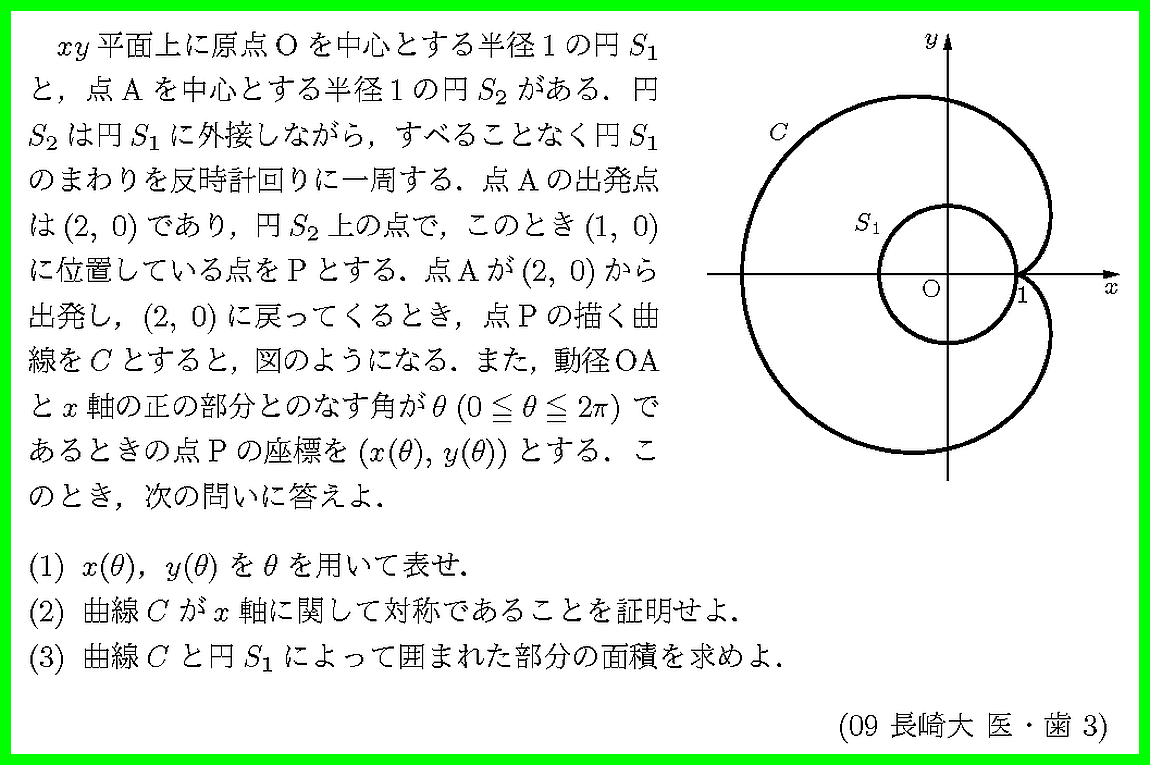
カージオイドのパラメータ表示と面積が問われています．