数学IIIチェック＆リピート　第5章　§2積分法の応用　4．体積(回転体)

数学IIIチェック＆リピート
パラメータ表示された曲線と面積 ← 体積(回転体) → 体積(非回転体)

問題文をクリックすると解答をみることができます．

体積(回転体) †

類題演習 †

ｘ軸まわりおよびｙ軸まわりの回転体の体積が問われています．

正確な計算力が求められています．

計算力が試されています．

面積，体積の計算により計算力が試されています．

中身の詰まったトーラス(円環面)の体積

逆関数と面積・体積を絡めて積分の基本を問うています．

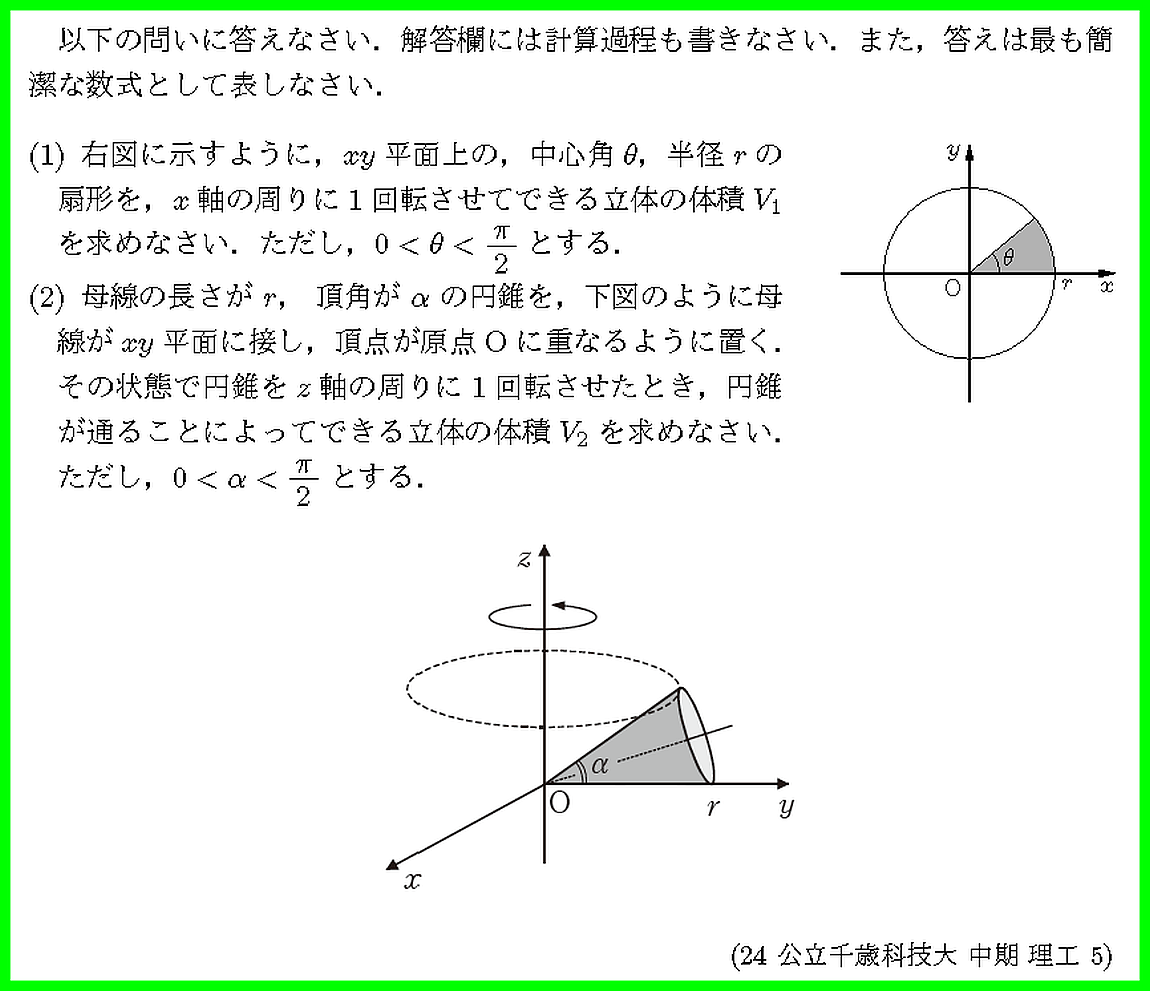
(１)は(２)のヒントになっています．

計算ミスに注意しましょう．

まずは接点の座標を求めましょう．

(３)は(４)のヒントです．

面積，体積の確認問題です．

体積の計算は2通り考えられます．

y軸まわりの回転体の体積が問われています．

体積計算で差がでそうです．

(２)で極値であることを増減表で示すか，ｙ’’を利用するか．

積分変数の扱いが問われています．

(２)は(３)の準備です．

面積，体積についての確認問題です．

傾き 1 の直線のまわりの回転体の体積です．

切り口は円の周および内部です．

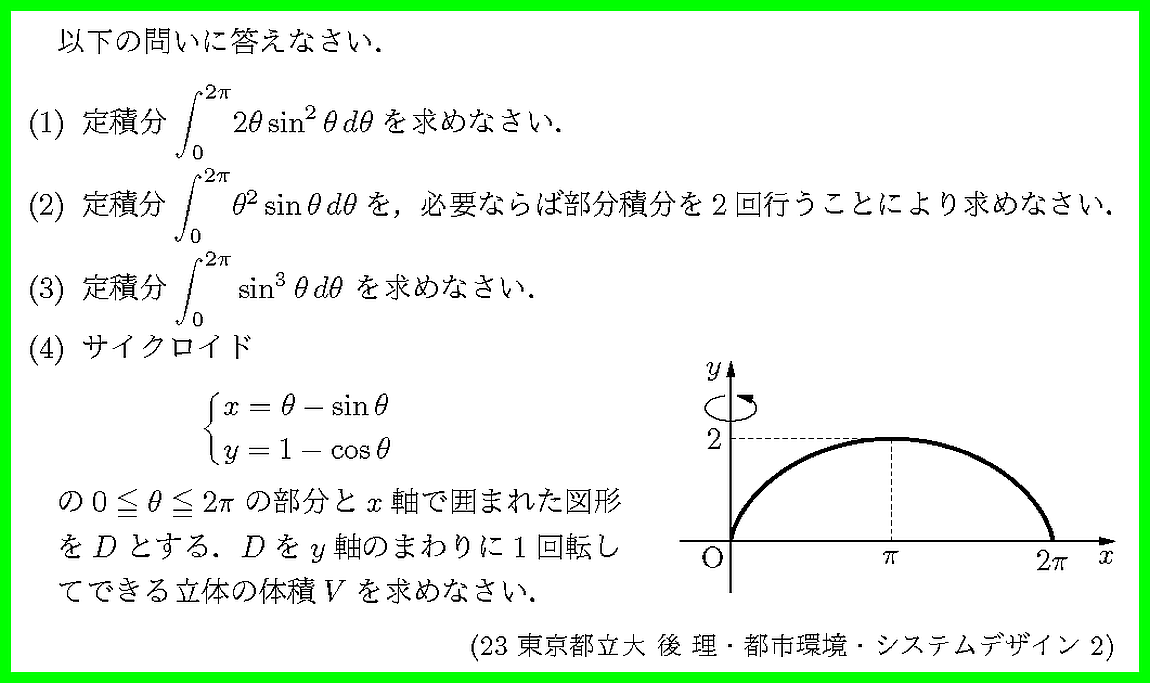
(１)(２)(３)は(４)の準備です．

体積の立式に困ることはないでしょう．あとは計算力が試されます．

(３)では場合分けが生じます．

Cは「カッシーニの卵形線」と呼ばれている曲線です．

(３)の積分がヤマでしょう．

微分積分の基本事項が問われています．

回転軸と垂直な平面による切り口を考えましょう．

半径ｒの値による場合分けが必要です．

(２)を利用してバームクーヘン型の積分公式を導きます．

(２) 増減表をかかなくても「f’=0 と f''の符号」で極値を判定することができます．

x軸のまわり，y軸のまわりの回転体の体積を問うています．

傾き -1 の直線のまわりの回転体の体積です．

PをS上に固定すると，線分PQは円錐の側面を描きます．

(３)の積分計算をどのように処理するか？

誘導にのりながら進みましょう．

接線，体積，最小値と微分法，積分法の基本事項が問われています．

(２)は頻出問題です．(３)では部分積分を繰り返します．計算力が問われています．

微分(微分可能性，最大値)と積分(体積)の融合問題となっています．

(２)回転体の切り口は，もとの図形の切り口を回転した図形です．

(４)は(５)の計算のヒントになっています．

(１)は2次方程式の解の配置，(２)はy軸まわりの回転体の体積です．確実に得点したい問題です．

手が止まることはありません．

計算力が試されています．

教科書の例題に載るような基本問題です．

体積と最小値を問う微積混合の標準問題です．

回転面を回転させたときの通過領域の体積とは凝った問題ですね．
回転軸に垂直な平面による切り口を考えていきましょう．

(１)内心の定義を確認しておきましょう．
(２)パラメータ表示のまま体積計算するか，
ｙ＝ｆ（ｘ）の関係式に直して体積計算するかわかれます．

ｙの範囲に対応するｘに注意して体積を計算しましょう．

面積，体積を通して積分の計算力が問われています．

教科書では例題として登場する問題です．

共通接線と回転体の体積を組み合わせた必須問題です．

y=x のまわりに回転して得られる回転体の体積が小問のひとつです．
かなりの計算力が要求されていることが分かります．

(１)は(２)の準備です．体積は２曲線の交点のｘ座標を求めることから始めましょう．

回転体の断面はもとの図形の切り口を回転させてできる図形です．