数学II・Bチェック＆リピート
3次方程式の解と係数の関係
← 虚数解をもつ3次方程式 →
±1の虚数立方根
問題文をクリックすると解答をみることができます．
虚数解をもつ3次方程式 †
類題演習 †
23 共通テスト本試験 II 4
２つの３次方程式の解の状態および共通解について問われています．
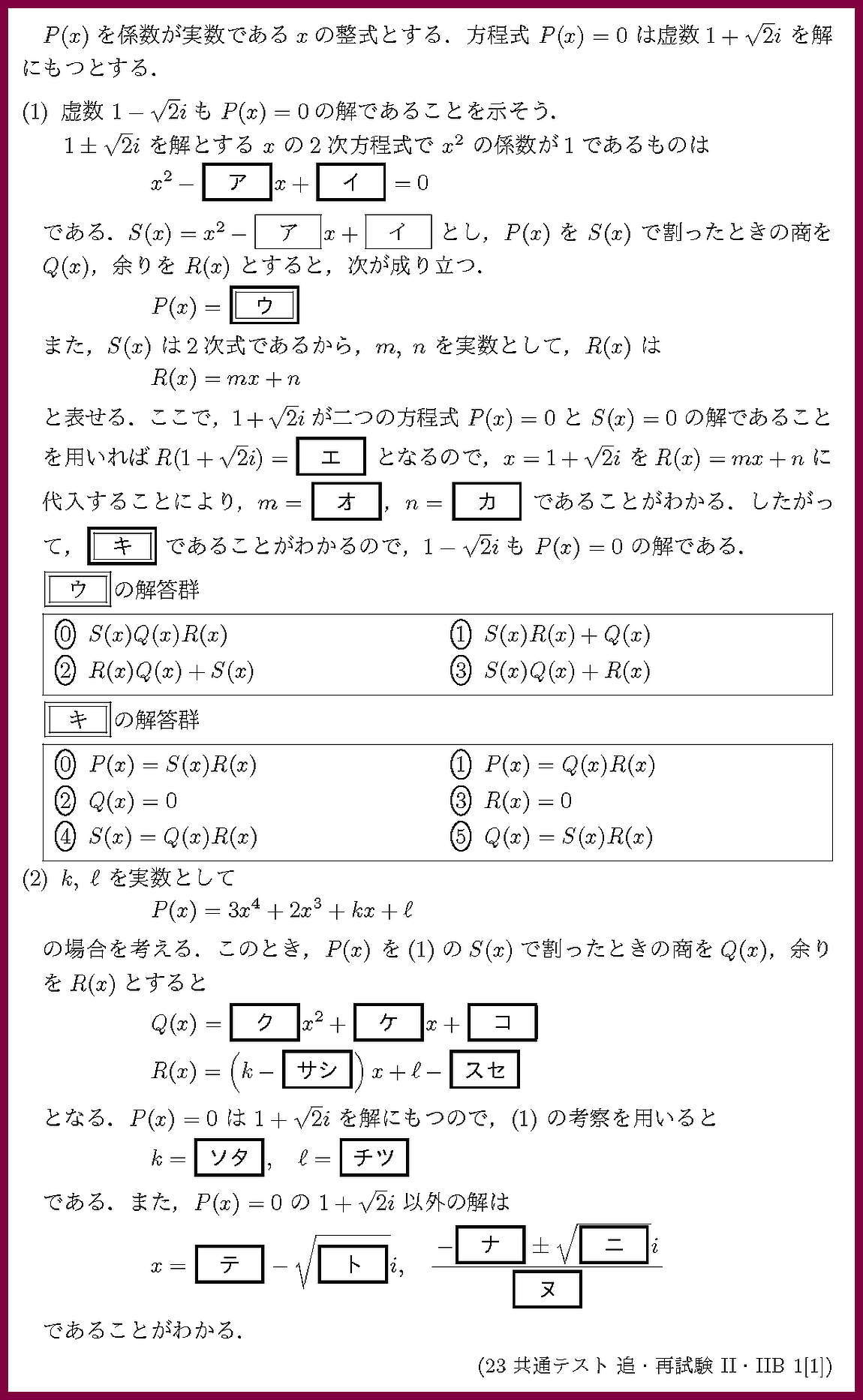
実数係数の方程式の共役解，整式のわり算について問われています．
３次方程式の解と係数の関係および虚数解をもつ3次方程式について問われています．
1-1problem.png "問題文をクリックしてみて下さい．")
与えられた方程式は実数を係数とする３次方程式です．
実数を係数とする高次方程式が虚数解をもつときはその共役複素数も解になります．
実数を係数とする高次方程式が虚数解をもつときはその共役複素数も解になります．
aの値を求めて方程式を確定させるか，解と係数の関係を利用するか．
実数を係数とする多項式f(x)に対し，
方程式f(x)=0が虚数解をもつならば，その共役複素数も解になります．
さらに本問では係数が有理数です．
ｐ，ｑが有理数のとき，ｐ＋ｑ×(無理数)＝０であることはｐ＝ｑ＝０と同値です．
普段当然のこととして使っている事柄を問われると戸惑う人もいるのでは？
![[PukiWiki]](image/kame.png "[PukiWiki]")
