数学IIIチェック＆リピート
定積分と不等式
← §2 積分法の応用：面積 →
接線・法線と曲線とで囲まれた部分の面積
問題文をクリックすると解答をみることができます．
面積 †
類題演習 †
円錐の側面を展開しましょう．
双曲線関数を用いて計算力が試されています．eの定義も登場します．
まずは曲線とｘ軸との交点のｘ座標を求めましょう．
(２)の計算は多いです．
微分と積分の計算力が問われています．
(２)のグラフにより状況がはっきり見えてきます．
(１)，(２)は独立した問題です．計算力が問われています．
概形をとらえて面積計算です．
点が取れるように配慮された問題です．
パラメータ表示された曲線の扱いを確認しておきましょう．
領域を求めるための(１)の誘導絶妙ですね．(３)は(４)のヒントです．これがないと積分はツライ．
グラフの概形を描いて面積を計算することにより微分積分の基本的な計算力が問われています．
手が止まることはないでしょう．
計算力が試されています．
(4)は面積の計算ですが，図形の概形を知るために微分処理が(1)(2)(3)で行われています．
(１)(２)(３)は(４)の準備で，(４)では面積と ｎlog ｎ の発散を比較しています．
計算力が問われています．
f(x)は奇関数です．対称性を利用しましょう．
1problem.png "問題文をクリックしてみて下さい．")
奇関数なので，グラフは原点に関して対称です．
幅広く微分積分について問うています．
最後の面積計算は少々鬱陶しい．
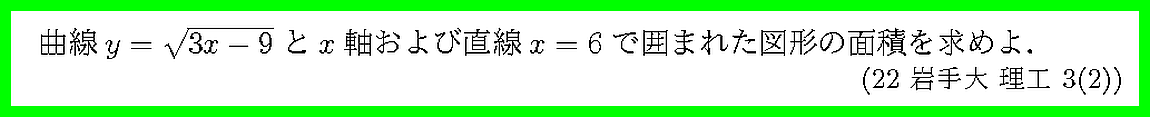
定義域にも注意しましょう．
kの偶，奇によりf(ｘ)の符号が決まります．
丁寧にグラフを描いて面積を求めよ，という問題です．
面積の最小値を問うています．素直に計算していけばよいでしょう．
被積分関数の符号は正です．
手は止まることなく進むことでしょう．
ｙで積分するか，ｘで積分するか分かれるでしょう．
(１)は a＾x の積分を示唆しています．
(２)の面積計算をこなした後，(３)ではヒントの式が使えるように式変形します．
計算をラクに済ませる工夫をしましょう．
面積の極限ではeの定義も絡んできます．
面積の基本問題です．
グラフをかいて2曲線の位置関係を示しましょう．
計算力が試される面積問題です．
面積を求める基本問題です．
グラフはy軸に関して対称です．さて，どんな図形が描かれるか？
(1)の概形をかいてホッコリ．
静岡大ならではの出題ですね．
![[PukiWiki]](image/kame.png "[PukiWiki]")
