数学IIIチェック&リピート
有理関数の積分(部分分数分解)
← 三角関数の積分 →
指数関数の積分
問題文をクリックすると解答をみることができます.
三角関数の積分 †

類題演習 †

(5)の計算準備として(1)(2)(4)が並んでいます.

(2)によりグラフの対称性に気づきます.(3)の積分計算に活かしましょう.

チェビシェフの多項式について問われています.

誘導無しでは(5)に辿り着くのは困難ですね.

(3)ではm=n,m≠nの場合分けが必要です.
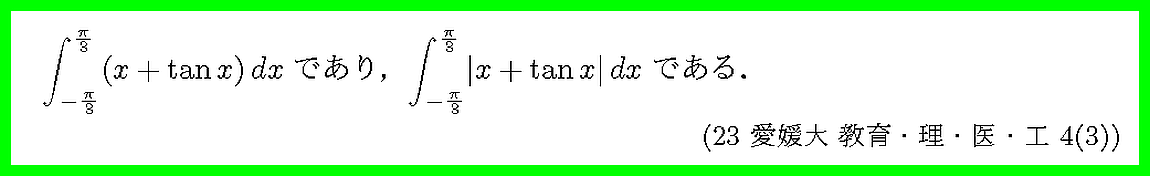
積分区間がy軸に関して対称なので偶関数・奇関数に着目しましょう.

計算力が問われています.

(1)(2)は(3)の準備です.

理工学部で(1)をやや易しくした問題が出題されています.

絶対値をはずすことから始めましょう.

被積分関数の次数下げを考えましょう.

2倍角,半角の公式を用いて次数下げを考えましょう.

2倍角の公式と部分積分法を用います.

置換積分を利用しましょう.
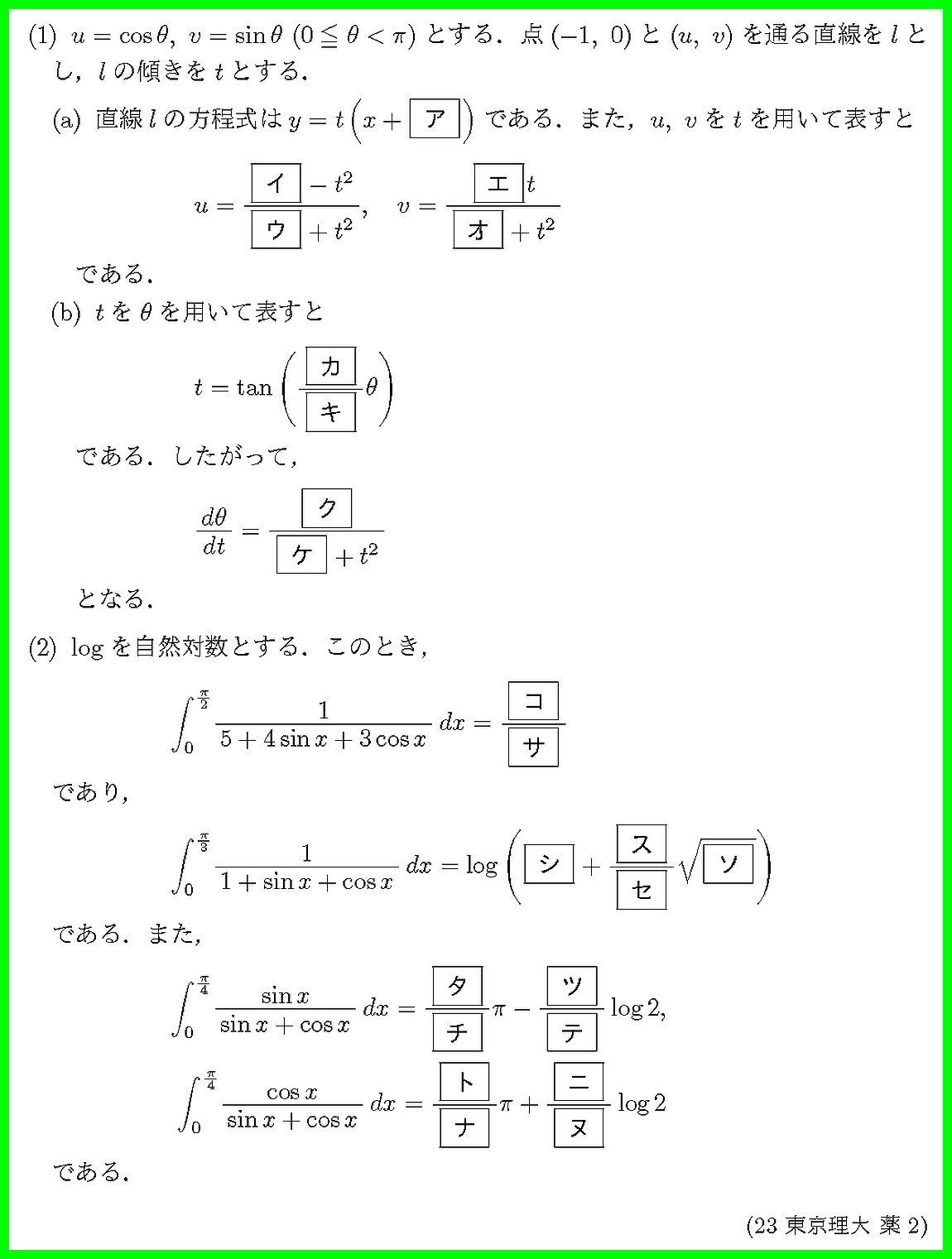
三角関数を有理関数に置換する積分が問われています.
(2)の最後の積分2つはセットにして扱います.

差がつく問題です.

2倍角の公式を用いながら式を整理しましょう.

半角の公式を用いて次数下げしましょう.
1-1problem.png)
半角の公式を用いましょう.

被積分関数の次数下げを考えます.

tanの2乗とcosの2乗の関係式を思い出しましょう.

tanの2乗とcosの2乗の関係式を思い出しましょう.置換積分法を用います.

直接計算するか,漸化式を考えるかになるでしょう.

偶関数であることに注意して積分区間を調整し,被積分関数は積和の公式を用いて変形しましょう.

前半は和を積に直す公式で出発します.後半は置換積分・部分積分の両方を使います.

難問です.対称性や周期性に着目し計算を減らす工夫をしましょう.

(1)は(2)のヒントであり,
(2)の積分をするためには絶対値をはず工夫をしなさいという出題者の意図がみえます.
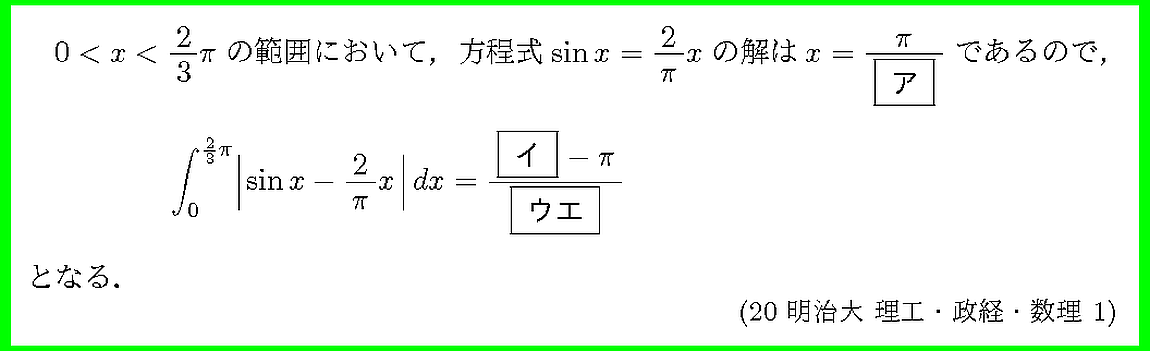
絶対値をはずすための誘導がついています.

後半の積分は置換積分法を用います.

(1)与えられた3条件からa,b,cの値が決まります.(2)は単純計算.

関数xをsin, cos の1次式で近似しようという問題です.
解く側としてはひたすら計算するのみです.

誘導にのりながら進んでいきましょう.
![[PukiWiki] [PukiWiki]](image/kame.png)
![[PukiWiki] [PukiWiki]](image/kame.png)